[편입] 2018 항공대학교 편입수학 기출문제 정답 및 해설 (풀이)
안녕하세요 수학올인입니다.
이번 포스팅에선 2018년 항공대학교 편입수학 기출문제의 정답과 풀이를 다뤄보겠습니다.
풀이는 전부 제 풀이이며, 따라서 오타나 오류가 있을 수 있습니다.
원본 시험지는 제가 공유하지 않으며, 항공대학교 입학처에서 확인하실 수 있습니다.
항공대의 경우 최근 2~3년 문제지만 공유하며, 년도가 바뀔 때마다 시험지를 입학처 홈페이지에서 삭제합니다.
따라서 시험지가 필요하신 분은 미리 입학처에서 다운로드를 받아두시기 바랍니다.
(항공대학교 입학처 - 편입학 - 지난기출문제)
2018 항공대학교 편입수학 기출문제 빠른 정답
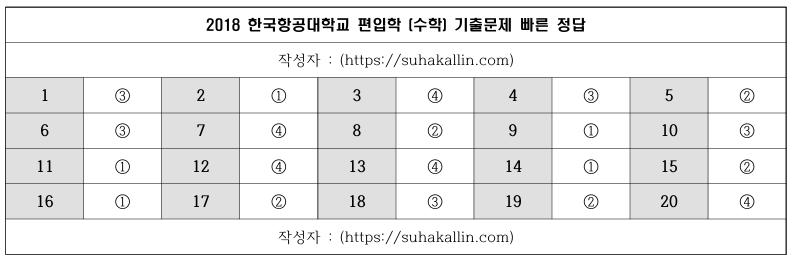
빠른 정답은 위 사진을 참고해 주시고, 아래는 문항별 풀이입니다.
2018 항공대학교 편입수학 기출문제 1번 풀이
ㄱ. 다항식이므로 수렴한다.
ㄴ. $x=t^2$으로 치환하면 분자와 분모의 차수가 같으므로 발산한다.
ㄷ. 분자의 차수가 분모의 차수보다 크므로 수렴한다.
ㄹ. 분자와 분모의 차수가 같으므로 발산한다.
이상에서 수렴하지 않는 것은 ㄴ, ㄹ이다.
2018 항공대학교 편입수학 기출문제 2번 풀이
ㄱ. 맞다.
ㄴ. 연속함수의 성질로부터 맞다.
ㄷ. 그래야 할 필요는 없다. 연속성이 미분가능성을 의미하지는 않는다.
이상에서 참인 것은 ㄱ, ㄴ이다.
2013 항공대학교 편입수학 기출문제 3번 풀이
식을 정리해보면 구하는 값은
$$(\det C)^2 + \det C + \frac{12}{\det C}$$
와 같은데, 계산을 통해 $\det C = 6$임을 알 수 있으므로 구하는 값은 $44$이다.
2018 항공대학교 편입수학 기출문제 4번 풀이
처음 주어진 두 점을 지나는 직선을 $l_1$, 나머지 두 점을 지나는 직선을 $l_2$라 하면
$$\begin{align}
& l_1 : (2t, t, -t) \\
& l_2 : (2t+1, t+1, 2t+1)
\end{align}$$
이다. 이제 두 직선의 방향벡터를 외적하여 얻은 벡터를 $n$이라 하면
$$n = (1,-2,0)$$
인데, 이를 법선벡터로 하고 $l_2$위의 한 점 $(1,1,1)$을 지나는 평면의 방정식은
$$P : x-2y+1 = 0$$
이다.
이제 구하는 두 직선사이의 거리는 평면 $P$와 $l_1$위의 한 점 $(0,0,0)$와의 거리와 같으므로
구하는 거리 $d$는
$$d = \frac{1}{\sqrt{5}}$$
이다.
2018 항공대학교 편입수학 기출문제 5번 풀이
양변을 $1+x^2$으로 나누면 주어진 미분방정식은
$$y' + \frac{x}{x^2 +1}y = -\frac{2x}{\sqrt{1+x^2}}$$
라는 일계 선형 미분방정식이 되므로 공식으로부터
$$\begin{align}
y &= e^{-\frac{1}{2}\ln(1+x^2)}\left(\int (-2x)dx + C\right) \\
&= \frac{1}{\sqrt{1+x^2}}\left(C - x^2\right) \\
&= -\frac{x^2}{\sqrt{x^2 + 1}}
\end{align}$$
이므로 $y(2) = -\frac{4}{\sqrt{5}}$이다.
2018 항공대학교 편입수학 기출문제 6번 풀이
점 $C$가 움직이는 경로는
$$r(t) = (t^2 , t)\quad (0\leq t\leq 1)$$
이므로 선적분의 정의대로 계산하면 주어진 선적분은
$$\begin{align}
\text{(Integral)} &= \int_0^1 (t^4 + t^2, -2t^3)\circ(2t, 1)dt \\
&= \int_0^1 2t^5 dt \\
&= \frac{1}{3}
\end{align}$$
이다.
2018 항공대학교 편입수학 기출문제 7번 풀이
ㄱ. 닮은 행렬의 성질로부터 참이다.
ㄴ. 행렬식의 성질로부터 참이다.
ㄷ. 고유치의 성질로부터 참이다.
이상에서 옳은 것은 ㄱ, ㄴ, ㄷ이다.
2018 항공대학교 편입수학 기출문제 8번 풀이
주어진 미분방정식의 보조방정식을 구해보면
$$r^2 + 2r+2=0$$
에서
$$r=-1\pm i$$
이므로
$$y=e^{-x}(c_1 \cos x+c_2\sin x)$$
가 성립한다.
이제 문제에서 주어진 두 초기조건을 이용하면
$$c_1=0, c_2=2e^{\frac{\pi}{2}}$$
이므로 정답은 2번이다.
2018 항공대학교 편입수학 기출문제 9번 풀이
변수변환
$$\begin{cases}
x+y=u\\
x-y=v
\end{cases}$$
를 이용하면 주어진 이중적분은
$$\begin{align}
\text{(Integral)} &= \frac{1}{2}\int_0^2\int_0^2 u^2 e^v dudv \\
&= \frac{4}{3}(e^2- 1)
\end{align}$$
이다.
2018 항공대학교 편입수학 기출문제 10번 풀이
사루스 공식을 이용하면
$$\det A = abc + 2 - (a+b+c) = 4$$
이다. 따라서 행렬식의 성질을 이용하면
$$\det(\text{adj}(A)) = (\det A)^2 = 16$$
이다.
2018 항공대학교 편입수학 기출문제 11번 풀이
행렬 $A$의 특성방정식이 제시되어있으므로 행렬 $A$의 고유치는
$$\lambda = \frac{1}{2}, \frac{3}{2}, \frac{4}{5}$$
이다. 따라서
$$\det A = \frac{1}{2}\times\frac{3}{2}\times\frac{4}{5} = \frac{3}{5}$$
이고 주어진 무한등비급수를 계산하면 구하는 값은
$$\sum_{n=0}^{\infty}\left(\frac{3}{5}\right)^n = \frac{5}{2}$$
이다.
2018 항공대학교 편입수학 기출문제 12번 풀이
부등식의 좌변의 식을 이차형식으로 표현했을 때 나타나는 대칭행렬은
$$A = \begin{pmatrix}
3 & -1 & 0 \\
-1 & 3 & 0 \\
0 & 0 & 8
\end{pmatrix}$$
이고, 이 행렬의 고유치는
$$\lambda = 2, 4, 8$$
이므로, 곡면
$$3x^2 - 2xy + 3y^2 + 8z^2 = 16$$
은 주축정리를 통해
$$2u^2 + 4v^2 + 8w^2 = 16$$
와 같다. 이는 정리하면
$$u^2 + 2v^2 + 4w^2 = 8$$
이고, 타원면이므로 이 내부의 넓이 $V$는
$$V = \frac{4}{3}\pi\times 2\sqrt{2}\times 2\times \sqrt{2} = \frac{32}{3}\pi$$
이다.
2018 항공대학교 편입수학 기출문제 13번 풀이
주어진 벡터장은 보존적이고 포텐셜함수는
$$f(x,y,z)=xe^{y}\cos z$$
이다. 따라서 선적분의 기본정리로부터 주어진 선적분은
$$\begin{align}
\text{(Integral)} &= f(x,y,z)\bigg|_{(0,0,0)}^{(1,2,0)} \\
&= e^2
\end{align}$$
이다.
2018 항공대학교 편입수학 기출문제 14번 풀이
문제의 조건으로부터
$$f'(x)=\frac{1}{x^2\sqrt{x^2 + 4}}$$
이다. 따라서 적분하면
$$\begin{align}
f(x) &= \int \frac{1}{x^2\sqrt{x^2 + 4}}dx \\
&= -\int \frac{t}{\sqrt{4t^2 + 1}}dt \quad \left(\frac{1}{x}=t\right) \\
&= -\frac{\sqrt{x^2 + 4}}{4x}+C
\end{align}$$
이고 초기조건을 이용하면 $C=0$이다. 따라서
$$f(2) = -\frac{1}{\sqrt{8}}$$
이다.
2018 항공대학교 편입수학 기출문제 15번 풀이
새로운 함수 $u(t) = y_1(t) + y_2(t)$를 생각하자.
그러면 문제에서 제시된 초깃값을 미분방정식에 각각 대입하면 $u'(0)=2$인데
이를 만족시키는 선택지는 2번 뿐이다.
2018 항공대학교 편입수학 기출문제 16번 풀이
직접 전개해보면
$$\begin{cases}
a+3b+2c=7\\
3a+2b+c=2\\
2a+b+3c=3
\end{cases}$$
에서 세 식을 전부 더하면
$$6(a+b+c)=12$$
에서 $a+b+c=2$임을 얻는다.
한편
$$T\begin{pmatrix}
1 \\
-1 \\
1
\end{pmatrix} = \begin{pmatrix}
a+b-c \\
a-b+c \\
-a+b+c
\end{pmatrix}$$
이므로, 구하는 모든 성분의 합은
$$a+b+c=2$$
이다.
2018 항공대학교 편입수학 기출문제 17번 풀이
주어진 지점은
$$x=\tan\frac{\pi}{3} = \sqrt{3}$$
이다. 이제 함수 $f(x)$의 식을 정리해보자.
$$\tan^{-1}x=a\quad\Longrightarrow \quad \tan a = x$$
라 하면
$$f(x)=\cos a = \frac{1}{\sqrt{x^2 + 1}}$$
이므로
$$f'(x) = -\frac{x}{(x^2 +1)^{\frac{3}{2}}}$$
이다. 따라서 구하는 값은
$$f'(\sqrt{3}) = -\frac{\sqrt{3}}{8}$$
이다.
2018 항공대학교 편입수학 기출문제 18번 풀이
장축, 단축의 길이를 각각 $2a, 2b$라 하면 문제의 조건으로부터
$$a=4, b=3, \frac{da}{dt} =\frac{3}{2}, \frac{db}{dt} = 2$$
이다. 이제 타원의 넓이는
$$S = ab\pi$$
이므로 양변을 $t$로 미분하면
$$\frac{dS}{dt} = \left(b\times \frac{da}{dt} + a\times \frac{db}{dt}\right)\pi$$
이고, 위에서 얻은 값을 전부 다 대입하면
$$\frac{dS}{dt} = \frac{25}{2}\pi$$
이다.
2018 항공대학교 편입수학 기출문제 19번 풀이
1번과 3번, 그리고 2번과 4번은 각각 같은 것에 대한 계산을 요구하고 있으므로
최대 두 번만 계산해보면 된다.
$$\frac{\overrightarrow{r}}{|r|} = \frac{1}{\sqrt{x^2+y^2+z^2}}(x,y,z)$$
임에 주목하여 직접 계산 노가다를 해보면
$$\overrightarrow{\nabla}\circ \frac{\overrightarrow{r}}{|r|}=\frac{2}{\sqrt{x^2+y^2+z^2}}$$
이고
$$\overrightarrow{\nabla}\times \frac{\overrightarrow{r}}{|r|} = 0$$
이므로 정답은 2번이다.
2018 항공대학교 편입수학 기출문제 20번 풀이
먼저 다음이 성립한다.
$$\frac{\pi^2}{6} = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots$$
이제 구하는 값을 $S$라 하고 식을 나열한 뒤 더하는 순서를 바꾸면
$$\begin{align}
\frac{\pi^2}{6} &= \frac{1}{1^2} + \frac{1}{3^2}+\frac{1}{5^2} + \cdots + \frac{1}{2^2}\left(\frac{1}{1^2} + \frac{1}{2^2} + \cdots\right) \\
&= S + \frac{1}{4}\times\frac{\pi^2}{6}
\end{align}$$
이므로 식을 정리하면
$$S=\frac{3}{4}\times\frac{\pi^2}{6}=\frac{\pi^2}{8}$$
이다.
마치며
이상으로 2018 항공대학교 편입수학 기출문제 정답 및 해설을 마치겠습니다.
오류, 오타 또는 궁금하신 점이 있으시면 댓글로 남겨주세요~
년도별 항공대학교 편입수학 정답 및 해설 (클릭시 이동)
(2012~2016년 항공대 해설은 제 블로그의 '항공대' 카테고리를 참고하세요.)
- 2017 항공대학교 편입수학 기출문제 정답 및 해설
- 2018 항공대학교 편입수학 기출문제 정답 및 해설 (현재)
- 2019 항공대학교 편입수학 기출문제 정답 및 해설
- 2020 항공대학교 편입수학 기출문제 정답 및 해설
- 2021 항공대학교 편입수학 기출문제 정답 및 해설
- 2022 항공대학교 편입수학 기출문제 정답 및 해설
- 2023 항공대학교 편입수학 기출문제 정답 및 해설
- 2024 항공대학교 편입수학 기출문제 정답 및 해설
'편입수학 기출문제 풀이 > 항공대' 카테고리의 다른 글
| [편입] 2020 항공대학교 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2024.03.25 |
|---|---|
| [편입] 2019 항공대학교 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2024.03.24 |
| [편입] 2017 항공대학교 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2024.03.22 |
| [편입] 2016 항공대학교 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2024.03.20 |
| [편입] 2015 항공대학교 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2024.03.19 |