함수가 극값을 가지면 그 지점에서 증감이 변할까?
안녕하세요 수학올인입니다.
이번 포스팅에서는 제목과 같이 어떤 미분가능한 함수 $f(x)$가 $x=a$에서 극값을
가진다면 $x=a$를 기준으로 함수 $f(x)$의 증감이 바뀌는지에 대해 다뤄보도록 하겠습니다.
그리고 본문에서는 상수함수는 제외하도록 하겠습니다.
이런 종류의 명제를 접했을 때 가장 먼저 해볼 수 있는 생각은 우리가 잘 알고 있는 함수들에 대해서
먼저 생각해보는 것입니다.
우리가 가장 잘 아는 함수는 당연히 다항함수겠죠? 그중에서 극값을 가지는 건 당연히
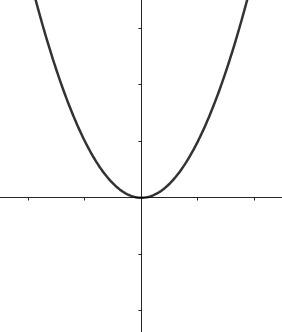
가장 만만한 이차함수일텐데요. 이차함수의 그래프를 확인하면 극값을 가지는 지점을 전후로
함수의 증감이 바뀌는걸 확인할 수 있습니다.
그럼 다른 함수는 어떨까요? 다항함수를 빼고 극값을 갖는 함수를 생각해 본다면...
삼각함수가 그 다음으로 떠오르는데요, 삼각함수의 그래프의 개형을 확인해 봐도 극값을 갖는
지점을 전후로 증감이 바뀌는걸 확인할 수 있습니다.

지금까진 뭔가 변형이 가해지지 않은 기본적인 형태의 함수에 대해서만 다뤄서 전부 맞았던 걸까요?
다항함수와 지수함수를 곱해서 얻은 함수라면 어떨까요?
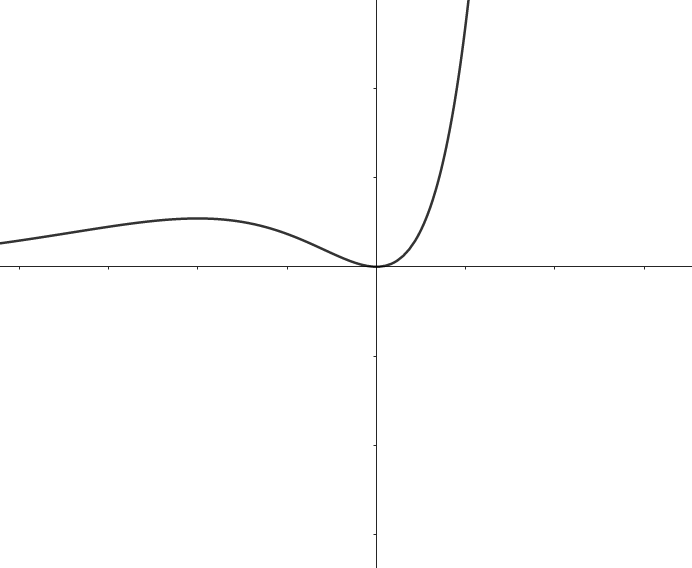
위 그래프는 곡선 $y=xe^x$의 그래프의 개형인데요, 어떤 함수의 기본적인 형태가 아닌 곱으로 연결된 함수에서도
동일하게 극값을 갖는 지점을 전후로 증감이 바뀜을 확인할 수 있습니다.
그럼 '미분가능한 함수 $f(x)$가 극값을 가지면 그 지점을 전후로 증감이 바뀐다.'라는 명제는 참일까요?
아쉽지만 주어진 명제는 거짓입니다. 물론 제가 뜸을 들이지 않았어도 이 포스팅을 썼다는 거 자체가
거짓임을 암시하고 있기도 하죠...ㅎㅎ
반례가 되는 함수도 이전 포스팅에서 다룬 함수와 비슷합니다.
반례
함수
$$f(x) = \begin{cases} x^4\left(1+\sin\left(\frac{1}{x}\right)\right) & (x\neq0) \\ 0 & (x=0) \end{cases}$$
에 대해 다음이 성립한다.
1. 함수 $f(x)$는 $x=0$에서 극소이다.
2. 함수 $f(x)$는 $x=0$을 기준으로 증가 → 감소 또는 감소 → 증가로 증감이 변하지 않는다.
이전 포스팅을 보셨다면 반례가 되는 함수가 비슷하게 생겼다는 생각이 드실 겁니다.
이전 포스팅에선 '무한히 진동한다'라는 점이 함수가 반례로 작용할 수 있도록 하는 핵심적인 이유였는데요.
이번에도 그 이유가 핵심적으로 작용하게 됩니다.
우선 1번부터 보여볼 텐데, 1번은 매우 매우 간단합니다. 왜냐하면 모든 실수 $x$에 대해
$$x^4\geq 0,\quad 1+\sin\left(\frac{1}{x}\right)\geq 0$$
이므로 결과적으로 모든 실수 $x$에 대하여 $f(x)\geq 0$입니다. 한편 $f(0)=0$이므로 부등식
$$f(x)\geq f(0)$$
이 성립하고, 극대-극소 정의로부터 함수 $f(x)$는 $x=0$에서 극소입니다.
그럼 이제 2번을 보여보도록 하겠습니다.
먼저 주어진 함수는 미분가능하므로, 직접 도함수를 구하면
$$f'(x)=4x^3\sin\left(\frac{1}{x}\right)+x^2-\cos\left(\frac{1}{x}\right)$$
이 성립합니다. 이제 수열
$$a_n=\frac{2}{\pi+4n\pi}>0$$
를 생각해 보면, $n\to\infty$일 때 $a_n\to 0$이고, 모든 자연수 $n$에 대하여 $f'(a_n)>0$이 성립합니다.
한편 비슷하게 $b_n \to 0$이면서 모든 자연수 $n$에 대하여 $f'(b_n)<0$이도록 하는 수열 $b_n>0$도
존재합니다. (한번 직접 찾아보세요!)
그럼 정리하면, 두 양의 실수 $a_n, b_n$은 원하는 만큼 $x=0$에 가깝게 할 수 있고 그와 동시에
$f'(a_n)>0, f'(b_n)<0$이라는 얘기네요.
그런데 무언가 이상하지 않나요? 만약 $x=0$에서 증감이 딱 떨어지게 증가에서 감소로,
혹은 감소에서 증가로 바뀐다면, $x=0$을 기준으로 양쪽에서 도함수의 부호가 달라야 합니다.
그런데 두 양의 실수 $a_n, b_n$은 원하는 만큼 $x=0$에 가깝게 할 수 있는 양수인데,
두 지점 중 한 지점에선 도함수가 양수, 한 지점에선 음수....
그렇죠. 모순입니다. 애초에 $x=0$을 기준으로 증감이 명확하게 바뀌지 않는다는 얘기입니다.
앞서 '무한히 진동한다'라는 점이 함수 $f(x)$가 반례로 작용할 수 있는 핵심적인 이유가 된다고
말씀드렸는데요. $x=0$ 근처에서 무한히 진동하며 증가와 감소를 바꾸고, $x=0$에선 극소인 상황인 겁니다.
말로는 잘 실감되지 않으니 그래프를 확인해 볼게요.

수식으로 표현했을 때 잘 이해가 안 되더라도, 시각적으로 확인하시면 이해가 잘 되실 겁니다.
$x=0$을 기준으로 증가에서 감소로, 또는 감소에서 증가로 딱 떨어지는 것이 아니라,
증감을 무한히 바꾸는 상황이죠. 따라서 우리는 상수함수를 제외하더라도
극값을 가진다는 사실이 증감의 변화를 만들지는 않음을 알 수 있습니다.
이번 포스팅은 여기까지입니다.
오류, 오타 또는 궁금하신 점이 있으시면 댓글로 남겨주세요~
'수학 (탐구)' 카테고리의 다른 글
| [수학] 도함수의 극한과 원함수의 극한의 관계 (0) | 2023.05.07 |
|---|---|
| [수학] 우함수는 항상 x=0에서 극값을 가질까? (0) | 2023.05.06 |
| [수학] 한 점에서 도함수가 양수지만 그 근방에서 증가하지 않는 함수 (3) | 2023.05.04 |
| [수학] 편미분을 이용한 음함수의 도함수, 이계도함수 공식 유도하기 (2) | 2023.05.03 |
| [수학] 이차 이하의 다항함수를 해로 가지는 함수방정식 (0) | 2023.05.02 |