2025학년도 6월 모의고사 수학 21번 풀이 (250621 풀이)
안녕하세요 수학올인입니다.
이번 포스팅에서는 2025학년도 6월 모의고사 수학 21번 문제를 다뤄보겠습니다.
문제

풀이
(가) 조건으로부터 $f'(2) = 0$임을 얻고, $x=2$가 함수 $f(x)$가 극값을 갖는 좌표중
가장 큰 (가장 오른쪽에 있는) 좌표임을 알 수 있다.
이제 방정식
$$f(x) = k$$
가 서로 다른 세 실근을 갖거나 서로 다른 네 실근을 가지려면 극대와 극소를 전부 가져야 한다.
또, 완전한 W모양의 선대칭인 사차함수의 경우 $k$의 최솟값이 존재하지 않으므로 배제해도 된다.
이제 다음과 같이 두 경우를 나누자.
i) 오른쪽 극솟값이 더 작은 경우
(나)조건으로부터 그래프는 다음과 같이 그려진다.

그런데, 가장 왼쪽의 극소점의 $x$좌표가 $x=1$이거나 극대점의 $x$좌표가 $x=1$인데
둘 중 어느 경우든 $f(0)=0$임에 모순이다. (이미 $y=\frac{8}{3}보다 위에 있으므로)
따라서 가능한 개형은 아래와 같은 경우이다.
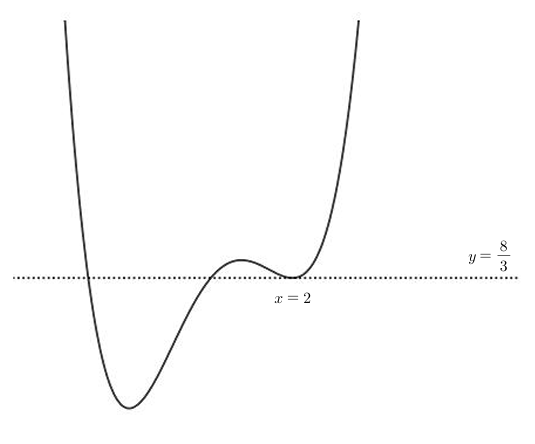
인수정리로부터
$$f(x) = (x-2)^2\left(x^2 + ax - \frac{2}{3}\right) + \frac{8}{3}$$
라고 쓸 수 있고
$$f'(1) = \frac{4}{3} - a = 0$$
에서 $a=\frac{4}{3}$임을 얻는다.
따라서
$$f(x) = (x-2)^2 \left(x^2 + \frac{4}{3}x - \frac{2}{3}\right) + \frac{8}{3}$$
이고 $f(3)=15$이다.
문제 난이도는 평이한데, 개인적인 의문으로는 (나)조건에서 $x$가 실수라는 언급이 없으면
복소근까지 포함하여 집합의 원소가 중근을 갖는 상황을 제외하면 항상 $4$가 되는게 아닌가 하는
생각이 듭니다. 방정식이 아니라 $f(x)$라는 다항함수로 표현했기 때문에 정의역이 실수 집합이 되므로
상관이 없는 것일까요...?
블로그에서 다룬 2025학년도 6월 모의고사 문제
(클릭시 이동)
- 2025학년도 6월 모의고사 수학 15번
- 2025학년도 6월 모의고사 수학 21번 (현재)
- 2025학년도 6월 모의고사 수학 22번
- 2025학년도 6월 모의고사 수학(미적분) 28번
- 2025학년도 6월 모의고사 수학(미적분) 29번
- 2025학년도 6월 모의고사 수학(미적분) 30번
'문제풀이 > 평가원, 교육청, 사관학교, 경찰대' 카테고리의 다른 글
| 2025학년도 6월 모의고사 수학 22번 풀이 (250622 풀이) (0) | 2024.06.04 |
|---|---|
| 2025학년도 6월 모의고사 수학 15번 풀이 (250615 풀이) (2) | 2024.06.04 |
| 2025학년도 6월 모의고사 수학(미적분) 28번 풀이 (250628 풀이) (0) | 2024.06.04 |
| 2025학년도 6월 모의고사 수학(미적분) 29번 풀이 (250629 풀이) (0) | 2024.06.04 |
| 2025학년도 6월 모의고사 수학(미적분) 30번 풀이 (250630 풀이) (0) | 2024.06.04 |