[수학] 장미곡선 성질 정리 (넓이, 그래프)
안녕하세요 수학올인입니다.
이번 포스팅에서는 장미곡선에 대해 다뤄보겠습니다.
장미곡선이라 함은 다음과 같은 극곡선을 말합니다.
$$\begin{align} r&=a\sin(k\theta) \\ r&= a\cos(k\theta)\end{align}$$
여기서 $a$와 $k$는 상수인데, $a$는 잎의 크기를 결정하고, $k$는 잎의 개수를 결정합니다.
그리고 식을 쓸 때 $\sin$을 쓰냐 $\cos$를 쓰냐의 차이는 회전의 의미를 나타냅니다.
(예를 들어, $r=\sin(2\theta)$와 $r=\cos(2\theta)$는 서로 회전된 관계에 있습니다.)
따라서 이 글에서는 전부 $\sin$을 사용하여 서술합니다.
아무튼, 잎의 크기와 개수라니 무슨 말인지 싶으실 것 같은데요, 아래 그림을 보시면 이해가 되실겁니다.

위 그림을 보면 곡선의 개형이 꽃잎처럼 그려지게 되는데, 이를 두고 각각의 고리를 잎이라고 표현합니다.
따라서 위에 말씀드린 내용을 다시 한 번 정리하면 $a$는 잎의 크기를 결정하고, $k$는 잎의 개수를 결정합니다.
그리고 주로 관심을 갖게 되는 것은 잎의 개수인데요, 왜냐하면 각각의 잎이 모두 대칭적이기 때문에
한 개의 잎에 대한 넓이를 구하게 되면 전체 곡선의 넓이를 구할 수 있기 때문입니다.
즉, 주된 관심사는 $k$가 됩니다.
자연스레 $k$에 무엇이 들어가냐에 따라 그림이 어떻게 달라지는지 궁금증이 생기게 되는데
i) $k$가 짝수라면 - 잎사귀가 $2k$개인 장미
ii) $k$가 홀수라면 - 잎사귀가 $k$개인 장미
iii) $k$가 유리수라면 - 한 주기의 길이가 유한한 폐곡선
iv) $k$가 무리수라면 - 길이가 무한한 곡선
의 형태를 띄게 됩니다. 이도 마찬가지로 그림을 통해 확인해보겠습니다.

이제 우리는 전체 내부 넓이를 구할 것인데, 이 계산 과정에서 대칭성을 이용할 것이므로
$k$의 값이 짝수일 때와 홀수일 때만을 생각합니다.
(실제로 문제에서도 정말 99.9%의 문제가 $k$가 홀/짝수일 때만을 다룹니다.)
장미 곡선의 내부 넓이 - $k$가 홀수
장미곡선
$$\begin{align} r&=a\sin(k\theta) \\ r&= a\cos(k\theta)\end{align}$$
에 대하여 $k$가 홀수인 경우 잎사귀가 $k$개이고, 잎사귀 한 개의 넓이 $S$는
$$\begin{align} S &= \frac{a^2}{2}\int_0^{\frac{\pi}{k}} \sin^2(k\theta)d\theta \\ &= \frac{a^2}{4}\int_0^{\frac{\pi}{k}} (1-\cos(2k\theta))d\theta \\ &= \frac{a^2 \pi}{4k} \end{align}$$
이므로, 전체 넓이는
$$k\times \frac{a^2 \pi}{4k} = \frac{a^2}{4}\pi$$
이다.
장미 곡선의 내부 넓이 - $k$가 짝수
장미곡선
$$\begin{align} r&=a\sin(k\theta) \\ r&= a\cos(k\theta)\end{align}$$
에 대하여 $k$가 짝수인 경우 잎사귀가 $2k$개이고, 잎사귀 한 개의 넓이 $S$는 위와 같다.
따라서 전체 넓이는 앞에 곱해지는 $k$가 $2k$로만 바뀌게 되므로
$$2k\times \frac{a^2 \pi}{4k} = \frac{a^2}{2}\pi$$
이다.
장미 곡선의 넓이 - 정리
위 내용을 홀/짝에 나누어 정리하면 아래 사진과 같습니다.
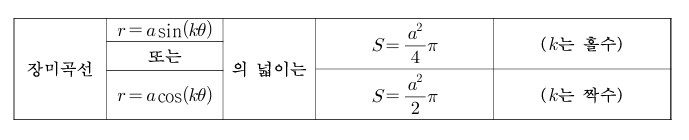
이상으로 이번 포스팅을 마치겠습니다.
'수학 (탐구)' 카테고리의 다른 글
| [수학] 교과내로 지수함수 다항함수 로그함수의 속도를 비교하는 방법 (0) | 2025.07.12 |
|---|---|
| [수학] 지수함수가 다항함수가 아님을 증명하는 두 가지 방법 (0) | 2025.04.24 |
| [수학] 어떤 연속함수의 이상적분이 수렴하면 함수의 극한은 0인가? (0) | 2024.05.11 |
| [수학] 심장형 곡선의 성질 정리 (넓이, 길이, 접선의 기울기, 회전체의 부피 등등) (0) | 2024.05.04 |
| [수학] 구의 일부분의 겉넓이 공식 (0) | 2024.05.02 |