2024학년도 10월 모의고사 수학 22번 풀이 (241022 풀이)
안녕하세요 수학올인입니다.
이번 포스팅에서는 2024학년도 10월 모의고사 수학 22번 문제를 다뤄보겠습니다.
문제

풀이
(가)조건에서
$$ g(x)=a(x-4)^2\left(x-\frac{21}{2}\right) $$
이다.
$0<x\leq 4$에서 주어진 그래프와 (나)조건을 해석하면 함수 $f(x)$의 그래프는 아래와 같다.
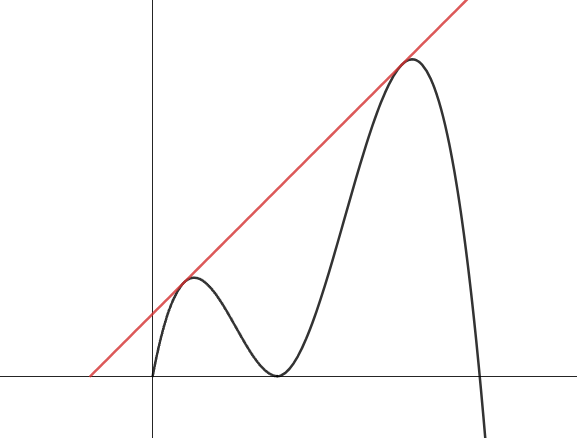
$h(x)=x^3 - 8x^2 + 16x$라 하고 직선과의 접점을 $t$라 하면
$$h'(t)=\frac{h(t)}{t+2}\quad\Longrightarrow\quad t=1$$
이고, 접선의 방정식(빨간색)은 $y=3(x+2)$이다.
마찬가지로 $y=g(x)$와 직선과의 접점을 $s$라 하면
$$g'(s)=\frac{g(s)}{s+2}\quad\Longrightarrow\quad s=8$$
이고 $g'(8)=3$이므로 (로그미분법을 이용하면 좋다.) $a=-\frac{3}{4}$이다.
따라서
$$g(x)=-\frac{3}{4}(x-4)^2\left(x-\frac{21}{2}\right)$$
이고
$$g(10)=\frac{27}{2}$$
이므로 구하는 값은 $29$이다.
상황은 비교적 간단한데, 계산이... 조금 힘든 문제였습니다.
이 풀이의 계산이 최적은 아닐 것 같은데, 조금 더 최적화를 할 필요가 있겠습니다.
블로그에서 다룬 2024학년도 10월 모의고사 문제
(클릭시 이동)
- 2024학년도 10월 모의고사 수학 15번
- 2024학년도 10월 모의고사 수학 22번 (현재)
- 2024학년도 10월 모의고사 수학(미적분) 28번
- 2024학년도 10월 모의고사 수학(미적분) 30번
'문제풀이 > 평가원, 교육청, 사관학교, 경찰대' 카테고리의 다른 글
| 2024학년도 10월 모의고사 미적분 28번 풀이 (241028 풀이) (0) | 2023.10.15 |
|---|---|
| 2024학년도 10월 모의고사 미적분 30번 풀이 (241030 풀이) (0) | 2023.10.14 |
| 2024학년도 10월 모의고사 수학 15번 풀이 (241015 풀이) (0) | 2023.10.12 |
| 2024학년도 6월 모의고사 수학 15번 풀이 (240615 풀이) (0) | 2023.10.10 |
| 2024학년도 6월 모의고사 미적분 30번 풀이 (240630 풀이) (0) | 2023.10.06 |