2025학년도 5월 모의고사 수학 22번 풀이 (250522 풀이)
안녕하세요 수학올인입니다.
이번 포스팅에서는 2025학년도 5월 모의고사 수학 22번 문제를 다뤄보겠습니다.
문제

풀이
가장 먼저 조건을 보면 $f(x) \geq 0$이어야 한다.
또, 조건으로 $g(x)$에 대한 정보를 추려보면
i) 임의의 실수 $x$에 대하여
$$\lim_{t \to 0}g(x+t) = g(x)$$
가 성립한다.
ii) $g(x)$는 불연속인 지점이 존재하며, 그 지점은 $f(x)$가 극값을 갖는 지점이다.
또, $g(x)$는 연속이 되는 각 구간에서 증가한다. 바꿔 말하면
$$g(x) = \begin{cases} f(x) & (f'(x) > 0) \\ -f(x) & (f'(x) \leq 0) \end{cases} $$
가 성립한다.
이제 함수 $g(x)h(x)$가 $x=k$에서 연속이 되려면
i) $g(x)$가 $x=k$에서 연속이고 $g(k)=0$인 것
ii) $h(x)$가 $x=k$에서 연속이고 $h(k) = 0$인 것
iii) 두 함수 각각 불연속이지만 곱했을 때 정의대로 연속이 되는 것. 즉,
$$\lim_{x\to k-} g(x)h(x) = \lim_{x\to k+} g(x)h(x) = g(k)h(k)$$
인 것
으로 세 경우가 있다.
이를 바탕으로 문제를 풀어보자.
가장 먼저 문제의 조건을 만족시키는 사차함수 $f(x)$의 그래프를 한 개 생각해보자.
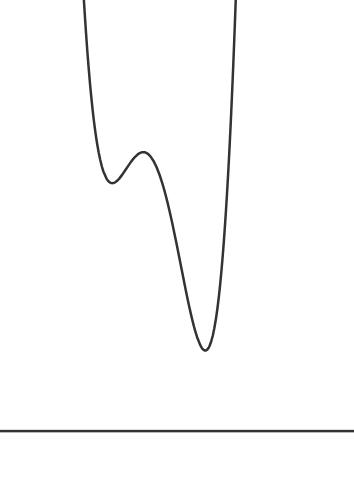
그러면 이를 바탕으로 $g(x)$는 다음과 같이 그려진다.

위의 개형에서 $g(x)$의 불연속점은 세 개이다.
이제 $h(x)$를 관찰해보면 $a$의 값을 조절해봤을 때
i) $h(x) = 0$이 되도록 하는 $x$는 많아봐야 한 개이다. ($x=-\frac{1}{2}$)
ii) $x=a$를 기점으로 절댓값은 같고 부호만 다른 지점도 많아봐야 한 개이다. 즉,
$$\lim_{x \to a-} h(x) = - \lim_{x\to a+} h(x)$$
(또는 반대 경우) 를 만족시키는 지점은 많아봐야 한 개이다. ($x=\frac{1}{2}$)
그럼 우리가 위에서 알아본 함수 $g(x)h(x)$가 $x=k$에서 연속이 될 조건을 이용해봤을 때
$g(x)$의 불연속점의 개수는 $3$이지만, $h(x)$를 곱해 불연속을 제거시킬 수 있는 지점은
많아봐야 두 개이다.
여기서 알 수 있는 사실은
1. $g(x)=0$ (즉, $f(x)=0$)인 지점이 존재한다. 따라서 $y=f(x)$는 $x$축과 접한다. ($x=s$라 하자.)
2. $h(x)=0$ 및 $h(x+)=-h(x-)$ (또는 부호반대)가 되는 두 실수 $x$와
함수 $f(x)$가 극값을 갖는 세 실수 $x$중 $x$축에 접하는 지점을 제외한 나머지 두 개가 일치한다.
따라서 2번에서 $a=\frac{1}{2}$이어야 하고, 함수 $f(x)$는 $x=-\frac{1}{2}, \frac{1}{2}, s$에서 극값을 가진다.
또, $g(0)=\frac{40}{3} > 0$이므로, $x=0$에서 함수 $f(x)$는 증가한다.
이를 전부 만족하는 $f(x)$의 개형은 다음과 같다.

식을 세워보면
$$f'(x) = 16\left(x^2 - \frac{1}{4}\right)(x-s)$$
이고 적분한 뒤 $g(0)=f(0) = \frac{40}{3}$을 이용하면
$$f(x) = 4x^4 - \frac{16s}{3}x^3 - 2x^2 + 4sx + \frac{40}{3}$$
이다. 이제 $g(s) = 0$을 이용하면
$$\frac{4}{3}s^4 - 2s^2 - \frac{40}{3} = 0$$
에서 $s=\pm 2$인데 음수인 경우는 모순이므로 $s=2$이다. 결과적으로
$$f(x) = 4x^4 - \frac{32}{3}x^3 - 2x^2 + 8x + \frac{40}{3}$$
이고
$$\begin{align} &g(1) = -f(1) = -\frac{38}{3} \\ &h(3) = -9\end{align}$$
이므로, 구하는 값은
$$g(1)\times h(3) = 114$$
이다.
개인적으로는 이번 시험지에서 가장 어려운 문항이 이 문항 아니었나 싶습니다.
블로그에서 다룬 2025학년도 5월 모의고사 문제
(클릭시 이동)
- 2025학년도 5월 모의고사 수학 13번
- 2025학년도 5월 모의고사 수학 14번
- 2025학년도 5월 모의고사 수학 15번
- 2025학년도 5월 모의고사 수학 22번 (현재)
- 2025학년도 5월 모의고사 수학(미적분) 28번
- 2025학년도 5월 모의고사 수학(미적분) 30번
'문제풀이 > 평가원, 교육청, 사관학교, 경찰대' 카테고리의 다른 글
| 2025학년도 6월 모의고사 수학(미적분) 29번 풀이 (250629 풀이) (0) | 2024.06.04 |
|---|---|
| 2025학년도 6월 모의고사 수학(미적분) 30번 풀이 (250630 풀이) (0) | 2024.06.04 |
| 2025학년도 5월 모의고사 수학(미적분) 30번 풀이 (250530 풀이) (0) | 2024.05.08 |
| 2025학년도 5월 모의고사 수학(미적분) 28번 풀이 (250528 풀이) (0) | 2024.05.08 |
| 2025학년도 5월 모의고사 수학 15번 풀이 (250515 풀이) (0) | 2024.05.08 |