편입수학 기출문제 풀이/항공대

[편입] 2016 항공대학교 편입수학 기출문제 정답 및 해설 (풀이)

수학올인 2024. 3. 20. 22:35

[편입] 2016 항공대학교 편입수학 기출문제 정답 및 해설 (풀이)

안녕하세요 수학올인입니다.

이번 포스팅에선 2016년 항공대학교 편입수학 기출문제의 정답과 풀이를 다뤄보겠습니다.

풀이는 전부 제 풀이이며, 따라서 오타나 오류가 있을 수 있습니다.

원본 시험지는 제가 공유하지 않으며, 항공대학교 입학처에서 확인하실 수 있습니다.

항공대의 경우 최근 2~3년 문제지만 공유하며, 년도가 바뀔 때마다 시험지를 입학처 홈페이지에서 삭제합니다.

따라서 시험지가 필요하신 분은 미리 입학처에서 다운로드를 받아두시기 바랍니다.

(항공대학교 입학처 - 편입학 - 지난기출문제)

2016 항공대학교 편입수학 기출문제 빠른 정답

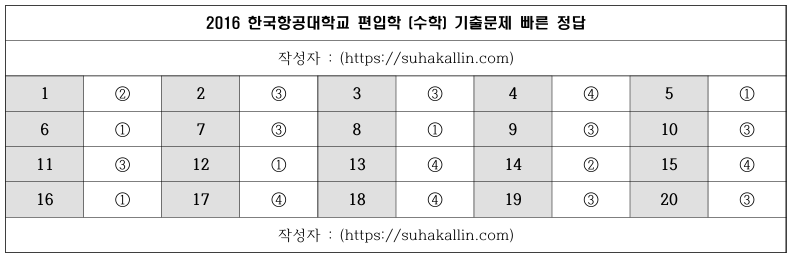
빠른 정답은 위 사진을 참고해 주시고, 아래는 문항별 풀이입니다.

2016 항공대학교 편입수학 기출문제 1번 풀이

로그 미분법을 이용하자. 양변에 로그를 취하면
$$\ln y = 3\ln x + \frac{1}{2}\ln(x^2 + 1) - 4\ln(3x+2)$$
에서 양변을 $x$로 미분하면
$$\frac{y'}{y} = \frac{x}{3} + \frac{x}{x^2 + 1} - \frac{12}{3x+2}$$
이므로 양변에 $y$를 곱하면
$$y' = \frac{x^3 \sqrt{x^2 + 1}}{(3x+2)^4}\left(\frac{x}{3} + \frac{x}{x^2 + 1} - \frac{12}{3x+2}\right)$$
이다.

2016 항공대학교 편입수학 기출문제 2번 풀이

$x=0$근방에서
$$\tan x \approx x + \frac{x^3}{3}$$
이 성립함을 이용하면 주어진 극한은
$$\lim_{x\to 0}\frac{2x^3}{3x^3} = \frac{2}{3}$$
이다.

2016 항공대학교 편입수학 기출문제 3번 풀이

시그마를 분배해서 계산하면
$$\begin{align}
\sum_{n=1}^{\infty} \frac{5}{n(n+1)} &= 5\sum_{n=1}^{\infty} \left(\frac{1}{n} - \frac{1}{n+1}\right) \\
&= 5
\end{align}$$
이고
$$\sum_{n=1}^{\infty} \frac{1}{3^n} = \frac{1}{2}$$
이므로 주어진 급수의 값은 $5+\frac{1}{2} = \frac{11}{2}$이다.

2016 항공대학교 편입수학 기출문제 4번 풀이

구하는 회전체의 부피 $V$는
$$\begin{align}
V &= 2\pi\int_0^4 x(4x-x^2)dx \\
&= \frac{128}{3}\pi
\end{align}$$
이다.

2016 항공대학교 편입수학 기출문제 5번 풀이

[풀이 1]
타원체
$$\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1$$
위의 점 $(x_0, y_0, z_0)$에서의 접평면의 방정식은
$$P : \frac{x_0 x}{a^2} + \frac{y_0 y}{b^2} + \frac{z_0 z}{c^2} = 1$$
임을 이용하면 구하는 접평면의 방정식은 1번이다.

[풀이 2]
주어진 점에서 함수
$$f(x,y,z) = \frac{x^2}{9} + \frac{y^2}{4} + \frac{z^2}{9} -3 =0 $$
의 경도벡터는
$$\nabla f = (2,-3,-2)$$
이므로, 이를 법선벡터로 하고 주어진 점을 지나는 평면의 방정식은 1번이다.

2016 항공대학교 편입수학 기출문제 6번 풀이

부분적분을 이용하면 주어진 적분은
$$\begin{align}
\text{(Integral)} &= x\tan^{-1} x\bigg|_0^{\frac{\pi}{4}} - \int_0^1 \frac{x}{x^2 + 1}dx \\
&= \frac{\pi}{4} - \frac{1}{2}\ln 2
\end{align}$$
이다.

2016 항공대학교 편입수학 기출문제 7번 풀이

(이 포스팅)을 참고하면 구하는 곡면의 넓이 $S$는
$$S = 2\pi \times 3 \times 3 = 18\pi$$
이다.

2016 항공대학교 편입수학 기출문제 8번 풀이

직선 $y=4x$와 곡선 $y=x^2$으로 둘러싸인 영역을 $D$라 하면, 영역 $D$의 넓이는 $\frac{32}{3}$이다.

따라서
$$\begin{align}
    \bar{x} &= \frac{3}{32}\iint_D xdydx \\
    &= \frac{3}{32}\int_0^4 x(4x-x^2)dx \\
    &= 2
\end{align}$$
이고
$$\begin{align}
    \bar{y} &= \frac{3}{32}\iint_D ydydx \\
    &= \frac{3}{64}\int_0^4 (16x^2 - x^4)dx \\
    &= \frac{32}{5}
\end{align}$$
이므로 정답은 1번이다.

2016 항공대학교 편입수학 기출문제 9번 풀이

(이 포스팅)을 참고하면 구하는 길이는 $16$이다.

2016 항공대학교 편입수학 기출문제 10번 풀이

문제에서 $(r,s,t)=(1,1,0)$일 때 $(x,y,z)=(2,1,0)$이다. 한편 연쇄법칙으로부터
$$u_s = u_x x_s + u_y y_s + u_z z_s$$
이고 위에서 얻은 $r, s, t, x, y, z$의 값을 전부 대입하면
$$\begin{align}
    u_x &= 32\\
    u_y &= 32 \\
    x_s &= 2\\
    y_s &= 2\\
    z_x &= 0
\end{align}$$
이므로 구하는 값은
$$32\times 2+32\times 2 = 128$$
이다.

2016 항공대학교 편입수학 기출문제 11번 풀이

구하는 각도는 두 벡터
$$\begin{align}
&\overrightarrow{\mathrm{OX}} = (-1,0,1) \\
&\overrightarrow{\mathrm{OY}} = (1,0,0)
\end{align}$$
의 사잇각과 같으므로 내적을 이용하면
$$\overrightarrow{\mathrm{OX}} \circ \overrightarrow{\mathrm{OY}} = -1 = \sqrt{2}\cos\theta$$
에서 식을 $\theta$에 대해 풀면 $\theta = \frac{3}{4}\pi$이다.

2016 항공대학교 편입수학 기출문제 12번 풀이

벡터 $\overrightarrow{\mathrm{OZ}}$가 두 벡터 $\overrightarrow{\mathrm{OX}}, \overrightarrow{\mathrm{OY}}$에 모두 수직이므로 내적을 이용하면
$$\begin{align}
& \overrightarrow{\mathrm{OZ}} \circ \overrightarrow{\mathrm{OX}} = a+c=0 \\
& \overrightarrow{\mathrm{OZ}} \circ \overrightarrow{\mathrm{OY}} = a+b+c=0
\end{align}$$
에서 둘을 빼면 $b=0$이다.

2016 항공대학교 편입수학 기출문제 13번 풀이

주어진 세 벡터가 기저벡터가 된다는 말은 세 벡터가 일차독립이라는 말과 같다.

따라서 세 벡터가 기저가 되지 않는 경우는 세 벡터가 일차종속인 경우이며
이는 세 벡터를 행으로 갖는 행렬
$$A = \begin{pmatrix}
2 & 1 & a \\
6 & 0 & b \\
4 & 1 & 5
\end{pmatrix}$$
의 행렬식이 $0$이라는 말과 같다. 직접 계산해보면
$$\det A = 6(a-5) + 2b = 0$$
이므로 등호가 성립하는 선지는 4번이다.

2016 항공대학교 편입수학 기출문제 14번 풀이

문제에서 제시된 고유치와 고유벡터로부터
$$\begin{align}
    A\begin{pmatrix}
1 \\
1
\end{pmatrix}  &= \begin{pmatrix}
1 \\
1
\end{pmatrix}  \\
A\begin{pmatrix}
1 \\
0
\end{pmatrix}&= \begin{pmatrix}
2 \\
0
\end{pmatrix}
\end{align}$$
이고, 이를 합쳐서 쓰면
$$A\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix} = \begin{pmatrix}
1 & 2 \\
1 & 0
\end{pmatrix}$$
이 성립한다. 이제 양변의 오른쪽에 행렬
$$B = \begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}$$
의 역행렬을 곱하면
$$A = \begin{pmatrix}
2 & -1 \\
0 & 1
\end{pmatrix}$$
임을 얻는다. 따라서 구하는 값은
$$a-b+c-d=2$$
이다.

2016 항공대학교 편입수학 기출문제 15번 풀이

어떤 행렬의 싱렬식의 값은 모든 고유치의 곱과 같으므로
$$\det A = 1\times 2\times 3 = 6$$
이다. 또, 행렬식의 성질로부터
$$\det A^{-1} = \frac{1}{\det A} = \frac{1}{6}$$
이다. 따라서 구하는 값은 $36$이다.

2016 항공대학교 편입수학 기출문제 16번 풀이

먼저 $\text{tr}(A^{-1})$은 행렬 $A^{-1}$의 모든 고유치의 합과 같다.
또, 행렬 $A^{-1}$의 고유치는 행렬 $A$의 고유치의 역수와 같음을 이용하자.

행렬 $A$의 고유치를 구해보면
$$\lambda = 1, 4, a, b$$
이다. 이때 $a, b$는 행렬
$$\begin{pmatrix}
2 & 5 \\
1 & 3
\end{pmatrix}$$
의 고유치, 즉 방정식 $\lambda^2 - 5\lambda + 1 = 0$의 두 근이다.

따라서 행렬 $A^{-1}$의 고유치는
$$\lambda = 1, \frac{1}{4}, \frac{1}{a}, \frac{1}{b}$$
이며 이들의 합을 구해보면 근과 계수의 관계로부터
\begin{align}
    \text{tr}(A^{-1}) &= 1 + \frac{1}{4} + \frac{1}{a} + \frac{1}{b} \\
    &= \frac{5}{4} + \frac{a+b}{ab} \\
    &= \frac{5}{4} + 5 \\
    &= \frac{25}{4}
\end{align}
이다.

2016 항공대학교 편입수학 기출문제 17번 풀이

a. 당연하게 맞다.

b. 행렬식의 값이 $0$이 아님과 동치이므로 맞다.

c. $\text{rank}$가 3임와 동치이고 이는 곧 행렬식의 값이 $0$이 아님과 같으므로 맞다.

d. 각 행이 일차독립임은 행렬식의 값이 $0$이 아님과 동치이므로 맞다.

이상에서 옳은 것은 $a, b, c, d$이다.

2016 항공대학교 편입수학 기출문제 18번 풀이

주어진 행렬 $A$를 선형변환으로 이해하면 임의의 $x \in \mathrm{R}^3$에 대하여
벡터 $y=Ax$는 $\text{Im}(A)$ (치역)에 속한다.

한편 치역은 열벡터의 일차결합으로 나타내어지므로 열공간의 기저를 찾기 위해
행렬 $A^T$에 기본행연산을 적용하여 기약행사다리꼴을 구해보면
$$\begin{align}
A^T &= \begin{pmatrix}
1 & 0 & 1 \\
1 & 1 & 0 \\
2 & 1 & 1
\end{pmatrix} \\
&\approx \begin{pmatrix}
1 & 0 & 1 \\
0 & 1 & -1 \\
0 & 0 & 0
\end{pmatrix}
\end{align}$$
이다. 즉, 선형변환 $A$의 치역의 기저는
$$\begin{pmatrix}
1 \\
0 \\
1
\end{pmatrix},\quad \begin{pmatrix}
0 \\
1 \\
-1
\end{pmatrix}$$
이다. 이제 이를 바탕으로 선지의 벡터가 치역에 속하는지 판단해볼텐데
이 둘의 일차결합으로 선지의 벡터를 나타내는 것은 비효율적이다.

우리는 이 두 벡터를 외적하여 얻은 벡터가 치역에 수직인 벡터라는 점을 이용하여
외적으로 얻은 벡터와 선지의 벡터를 내적하여 0이 되는 선지를 찾을 것이다.
(내적이 0이라는 말은 곧 이 벡터에 수직이고 곧 치역에 속한다는 말이므로.)
둘을 외적해보면 치역에 수직인 벡터 $n$은
$$n = \begin{pmatrix}
-1 \\
1 \\
1
\end{pmatrix}$$
이고 이 벡터와 내적이 $0$인 벡터는 4번이다.

2016 항공대학교 편입수학 기출문제 19번 풀이

$\text{rank}$의 성질로부터
$$\text{rank}(A) = \text{rank}(A^T) = \text{rank}(AA^T)$$
가 성립하고, 차원정리로부터
$$\dim(\text{Null}(A)) = 5-\text{rank}(A) = 2$$
가 성립하므로 구하는 값은 $3+2+3=8$이다.

2016 항공대학교 편입수학 기출문제 20번 풀이

주어진 연립방정식을 행렬표현으로 나타내면
$$\begin{pmatrix}
1 & 1 \\
1 & -1 \\
2 & 1
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix} = \begin{pmatrix}
1 \\
0 \\
2
\end{pmatrix}$$
이다. 이제 최소제곱해를 구하는 공식으로부터
$$\begin{pmatrix}
6 & 2 \\
2 & 3
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix} = \begin{pmatrix}
5 \\
3
\end{pmatrix}$$
를 풀면
$$x=\frac{9}{14}, y=\frac{4}{7}$$
임을 얻는다.

마치며

이상으로 2016 항공대학교 편입수학 기출문제 정답 및 해설을 마치겠습니다.

오류, 오타 또는 궁금하신 점이 있으시면 댓글로 남겨주세요~