[편입] 2016 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설 (풀이)
안녕하세요 수학올인입니다.
이번 포스팅에선 2016년 중앙대학교(수학과) 편입수학 기출문제의 정답과 풀이를 다뤄보겠습니다.
풀이는 전부 제 풀이이며, 따라서 오타나 오류가 있을 수 있습니다.
원본 시험지는 제가 공유하지 않으며, 중앙대학교 입학처에서 확인하실 수 있습니다.
(중앙대학교 입학처 - 편입학 - 기출문제)
2016 중앙대학교 편입수학 기출문제 빠른 정답

빠른 정답은 위 사진을 참고해 주시고, 아래는 문항별 풀이입니다.
2016 중앙대학교 편입수학 기출문제 1번 풀이
유리화를 하면
$$\frac{1}{\sqrt{3n + \sqrt{2n}} - \sqrt{3n}} = \frac{\sqrt{3n + \sqrt{2n}} + \sqrt{3n}}{\sqrt{2n}}$$
이므로 주어진 극한값은
$$2 \times \sqrt{\frac{3}{2}} = \sqrt{6}$$
이다.
2016 중앙대학교 편입수학 기출문제 2번 풀이
테일러전개를 이용하면
$$\sin x \approx x - \frac{x^3}{6}$$
이므로 구하는 극한값은 $6$이다.
2016 중앙대학교 편입수학 기출문제 3번 풀이
주어진 적분은
\begin{align}
\text{(Integral)} &= \frac{1}{2}\int_0^1 e^tdt \quad (1-x^2 = t) \\
&= \frac{e-1}{2}
\end{align}
이다.
2016 중앙대학교 편입수학 기출문제 4번 풀이
주어진 적분은
$$\begin{align}
\text{(Integral)} &= \frac{1}{2}\int_0^5 \sqrt{t}dt \quad (x^2 - 4 = t) \\
&= \frac{5\sqrt{5}}{3}
\end{align}
$$
이다.
2016 중앙대학교 편입수학 기출문제 5번 풀이
감마함수를 이용하면 주어진 적분은
$$\text{(Integral)} = \Gamma (3) = 2$$
이다.
2016 중앙대학교 편입수학 기출문제 6번 풀이
$f(x,y)=x^2+y^2-\cos xy = 0$이라고 하고 음함수의 미분법을 활용하면
$$\begin{align}
\frac{dy}{dx} &= -\frac{f_x}{f_y} \\
&= -\frac{2x+y\sin xy}{2y+x\sin xy}
\end{align}$$
이다.
2016 중앙대학교 편입수학 기출문제 7번 풀이
구하는 넓이는 두 벡터 $\mathrm{AB}, \mathrm{AC}$를 외적하여 얻은 벡터의 크기와 같다.
직접 외적을 계산해보면
$$\mathrm{AB}\times\mathrm{AC}=(23,-1,-7)$$
이므로 크기를 구하면 $\sqrt{579}$이다.
2016 중앙대학교 편입수학 기출문제 8번 풀이
$x=\sin^2 t$로 치환하면 주어진 적분은
$$\begin{align}
\text{(Integral)} &= \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \sqrt{\frac{1-\sin^2 t}{\sin^2 t}}2\sin t\cos tdt \\
&= \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} 2\cos^2 tdt \\
&= \frac{\pi}{4}-\frac{1}{2}
\end{align}$$
이다.
2016 중앙대학교 편입수학 기출문제 9번 풀이
주어진 세 벡터가 일차종속이려면 주어진 세 벡터를 열로 갖는 행렬
$$A = \begin{pmatrix}
1 & 3 & 1 \\
2 & 7 & h \\
1 & 2 & 4 \\
\end{pmatrix}
$$
의 행렬식이 $0$이면 된다. 직접 행렬식을 구해보면
$$\det A = 1+h$$
이므로 $h=-1$이다.
2016 중앙대학교 편입수학 기출문제 10번 풀이
주어진 행렬에 곱하는 벡터
$$\begin{pmatrix}
1 \\
1 \\
\end{pmatrix}
$$
은 주어진 행렬의 고유치 $\lambda = 2$에 대응하는 고유벡터이다.
따라서 주어진 행렬을 $A$라 하면
$$A\begin{pmatrix}
1 \\
1 \\
\end{pmatrix} = 2^{10}\begin{pmatrix}
1 \\
1 \\
\end{pmatrix}$$
이고, 따라서 $a+b=2^{11}$이다.
2016 중앙대학교 편입수학 기출문제 11번 풀이
주어진 기약행사다리꼴의 첫쨰, 둘째, 넷째행의 일차결합으로 다섯번째 행을 만들면
$$-2\begin{pmatrix}
1 \\
0 \\
0 \\
\end{pmatrix}
-3 \begin{pmatrix}
0 \\
1 \\
0 \\
\end{pmatrix}
- 6 \begin{pmatrix}
0 \\
0 \\
1 \\
\end{pmatrix}
= \begin{pmatrix}
-2 \\
-3 \\
-6 \\
\end{pmatrix}
$$
이다.
따라서 주어진 세 벡터를 순서대로 $v_1, v_2, v_3$라 하면 원래 행렬의 다섯번째 행 $v$는
$$v = -2v_1 -3v_2 -6v_3$$
가 성립한다. 따라서 원래 행렬의 $(2,5)$성분은 $v$의 $2$번째 성분과 같으므로
$$A(2,5) = -2\times(-1) -3\times(-1) + 6\times(-2) = -7$$
이다.
2016 중앙대학교 편입수학 기출문제 12번 풀이
산술기하평균 부등식을 이용하면
$$\begin{align}
1 &\geq x^2 + 4y^2 \\
&\geq 2\sqrt{4x^2y^2} \\
&= 4|xy|
\end{align}$$
에서
$$-\frac{1}{4}\leq xy \leq \frac{1}{4}$$
이다. 즉,
$$-\frac{\sqrt{2}}{2}\leq \sin(\pi xy)\leq \frac{\sqrt{2}}{2}$$
가 성립하므로, 최댓값과 최솟값의 차는 $\sqrt{2}$이다.
2016 중앙대학교 편입수학 기출문제 13번 풀이
주어진 두 벡터의 일차결합으로
$$\begin{pmatrix}
8 \\
11
\end{pmatrix} = 2\begin{pmatrix}
1 \\
1
\end{pmatrix} + 3\begin{pmatrix}
2 \\
3
\end{pmatrix}$$
로 나타낼 수 있다. 따라서 선형변환의 선형성으로부터
$$\begin{pmatrix}
a \\
b \\
c
\end{pmatrix} = 2\begin{pmatrix}
1 \\
0 \\
2
\end{pmatrix} + 3\begin{pmatrix}
1 \\
-1 \\
4
\end{pmatrix}$$
임을 알 수 있으므로
$$a+b+c=2\times 3 + 3\times 4 = 18$$
이다.
2016 중앙대학교 편입수학 기출문제 14번 풀이
$12+3y=k$라 하면 $k$가 최소가 되는 상황은 직선 $12+3y=k$의 $y$절편이 최소가 될 때이고
결국 그림을 생각해보면 아래 그림과 같이 접하는 상황일 때가 된다.
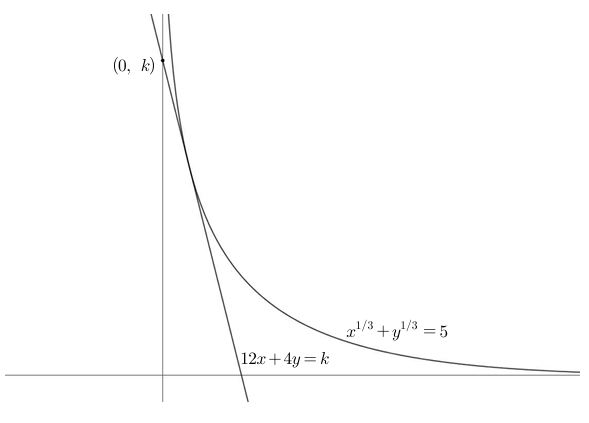
따라서 접점을 찾기 위해 성망형 곡선의 기울기가 $-4$인 지점을 찾아보면 음함수 미분법으로부터
$$y'=-\left(\frac{y}{x}\right)^{\frac{2}{3}} = -4$$
에서 $y=8x$임을 얻는다. 이를 성망형 곡선의 식에 대입해보면
$$3x^{\frac{1}{3}} = 5\quad\Longrightarrow\quad \begin{cases}
x=\frac{125}{27} \\ y=\frac{1000}{27}
\end{cases}$$
이므로 $k$의 최솟값은
$$\frac{500}{9} + \frac{1000}{9} = \frac{500}{3}$$
이다.
2016 중앙대학교 편입수학 기출문제 15번 풀이
두 직선의 방향벡터를 외적하여 얻은 벡터를 구해보면
$$n = (4,-5,-7)$$
이다. 이를 법선벡터로 하고 두 번째 직선 위의 한 점 $(2,4,-3)$을 지나는 평면의 방정식은
$$P : 4x-5y-7z=9$$
이다. 이제 이 평면과 첫 번째 직선 위의 한 점 $(1,0,0)$사이의 거리가 구하는 두 직선 사이의 거리이므로
구하는 거리 $d$는
$$d= \frac{|4-9|}{\sqrt{16+25+49}} = \frac{\sqrt{10}}{6}$$
이다.
2016 중앙대학교 편입수학 기출문제 16번 풀이
구하는 값은 행렬식의 값과 같으므로 $\det A = -28$이다.
2016 중앙대학교 편입수학 기출문제 17번 풀이
임의의 자연수 $m$에 대하여
$$\det I_m = 1$$
이므로, 블록행렬의 행렬식을 이용하면
$$(-1)^{mn}\det J_n$$
이 구하는 행렬식의 값과 같다.
이제
$$\det J_2 = \det J_3 = -1$$
이므로 $n= 2, 3$일 때
$$\frac{n(n-1)}{2} = -1$$
이고,
$$\det J_4 = \det J_5 = 1$$
이므로 $n= 4, 5$일 때
$$\frac{n(n-1)}{2} = 1$$
이다. 따라서 $-1$의 지수부분에 $\frac{n(n-1)}{2}$가 있는 2번이 정답이다.
2016 중앙대학교 편입수학 기출문제 18번 풀이
주어진 기저에서 벡터 $3b_1 - 4b_2$의 좌표벡터는 $(3, -4, 0)$이다. 따라서
$$\begin{pmatrix}
0 & -6 & 1 \\
0 & 5 & -1 \\
1 & -2 & 7
\end{pmatrix}\begin{pmatrix}
3 \\
-4 \\
0
\end{pmatrix} = \begin{pmatrix}
24 \\
-20 \\
11
\end{pmatrix}$$
이므로
$$\begin{cases}
x=24 \\
y=-20\\
z=11
\end{cases}$$
이다. 따라서 구하는 값은
$$x+y+z=15$$
이다.
2016 중앙대학교 편입수학 기출문제 19번 풀이
주어진 극곡선을 전부 직교좌표계의 곡선으로 바꿔보면
$$r=-2\cos\theta \quad\Longrightarrow\quad (x+1)^2 + y^2 = 1$$
이고
$$r^2-2r\cos\theta = 3\quad\Longrightarrow\quad (x-1)^2 + y^2 = 4$$
이다. 이제 문제의 상황을 그림으로 나타내보면 다음과 같다.
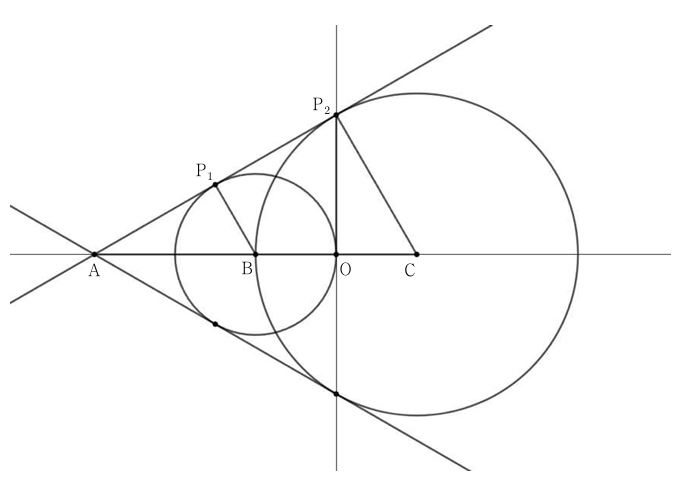
이때 $\rm{B}, \rm{C}$는 각각 두 원의 중심이고, $\rm{P_1}, \rm{P_2}$는 $\rm{B}, \rm{C}$ 각각에서
접선에 내린 수선의 발이다.
그러면 두 삼각형 $\rm{ABP_1}, \rm{ACP_2}$에 대하여
$$\overline{\rm{AB}}:\overline{\rm{AC}}=\overline{\rm{BP_1}}:\overline{\rm{CP_2}}$$
에서 $\overline{\rm{BP_1}}=1, \overline{\rm{CP_2}}=2$이므로 점 $\rm{A}$의 $x$좌표를 $a$라 하면
$$\overline{\rm{AC}}=2\overline{\rm{AB}}\quad\Longrightarrow\quad 1-x=2(-1-x)$$
에서 $x=-3$이다. 따라서 $\rm{A}(-3, 0)$이다.
그러면 삼각형 $\rm{ABP_1}$에 피타고라스 정리를 이용하면 $\overline{\rm{AP_1}}=\sqrt{3}$임을 얻는다.
이제 두 삼각형 $\rm{ABP_1}, \rm{AOP_2}$에 대하여
$$\overline{\rm{AP_1}}:\overline{\rm{BP_1}}=\overline{\rm{AO}}:\overline{\rm{OP_2}}$$
이고, 이를 풀면
$$3 = \sqrt{3} \times \overline{\rm{OP_2}}\quad\Longrightarrow\quad \overline{\rm{OP_2}}=\sqrt{3}$$
이다. 한편 대칭성을 이용하면 구하는 넓이는
$$2\times\frac{1}{2}\times\overline{\rm{AO}}\times \overline{\rm{OP_2}}=3\sqrt{3}$$
이다.
2016 중앙대학교 편입수학 기출문제 20번 풀이
변수변환
$$\begin{cases}
x+y=u\\
x-y=v
\end{cases}$$
를 이용하면 주어진 이중적분은
$$\begin{align}
\text{(Integral)} &= \frac{1}{2}\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \int_0^1 v\cos uv dudv \\
&= \frac{\sqrt{3}-1}{4}
\end{align}$$
이다.
2016 중앙대학교 편입수학 기출문제 21번 풀이
구 $S$의 내부를 $E$라 하자. 발산정리를 이용하면 주어진 면적분은
$$\begin{align}
\text{(Integral)} &= \iiint_E (2x+x+1)dV \\
&= \frac{4}{3}\pi\times 2^3 \\
&= \frac{32}{3}\pi
\end{align}$$
이다.
2016 중앙대학교 편입수학 기출문제 22번 풀이
주어진 평면의 법선벡터를 방향벡터로 갖고 점 $(4,4,1)$을 지나는 직선의 방정식을 구해보면
$$l(t) = (t+4,3t+4,-2t+1)$$
이다. 이제 주어진 점은 $t=0$일 때이고, 이 직선이 평면의 방정식과 만나는 순간을 구해보면
$$(t+4)+3(3t+4)-2(-2t+1)=7$$
에서
$$t=-\frac{1}{2}$$
이다.
따라서 대칭점은 동일한 간격만큼 더 진행한 $t=-1$일 때이며 대입하면 대칭점의 좌표는
$$l(-1) = (3, 1, 3)$$
이다.
2016 중앙대학교 편입수학 기출문제 23번 풀이
22번의 점과 평면이 동일하게 주어져있으므로, 문제 상황을 그대로 이용할 수 있다.
문제를 풀기 위한 세팅을 그림으로 표현하면 다음과 같다.
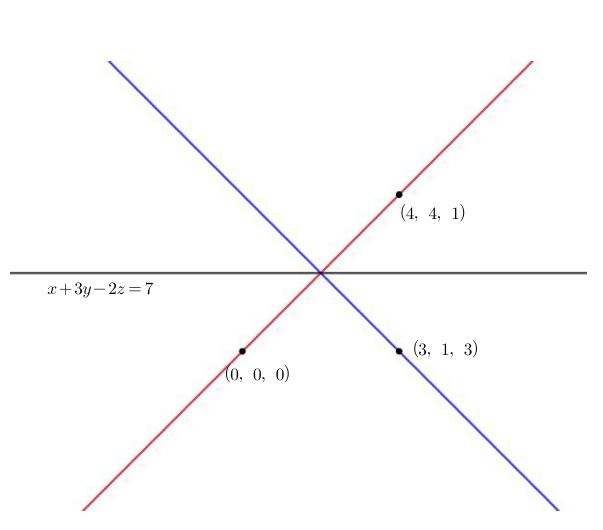
이를 글로 표현해보면
i) 원점과 점 $(4,4,1)$을 지나는 직선을 구한다. (빨간색 직선)
ii) 빨간 직선과 평면의 교점을 구한 뒤, 이 점과 $(3,1,3)$을 지나는 직선을 구한다. (파란색 직선)
iii) 파란색 직선과 $xz$명편의 교점을 구한다.
와 같다.
빨간색 직선을 구해보면
$$l_1(t) = (4t,4t,t)$$
이고, 이 직선과 평면의 교점을 구해보면
$$4t+3(4t)-2(t)=7$$
에서 $t=\frac{1}{2}$일 때이므로
$$l_1\left(\frac{1}{2}\right) = (2,2,1)$$
이 평면과 빨간색 직선의 교점이다.
다음으로 파란색 직선을 구해보면 두 점 $(2,2,1),(3,1,3)$을 지나야 하므로
$$l_2(t) = \left(t+2,-t+2,\frac{5}{2}t+\frac{1}{2}\right)$$
이다. 이제 이 직선이 $xz$평면과 만나는 순간은 $y$좌표가 0인 순간이므로 $t=2$이다.
즉,
$$l_2(2)=\left(4,0,\frac{11}{2}\right)$$
가 구하는 점의 좌표이다.
2016 중앙대학교 편입수학 기출문제 24번 풀이
(가)
$$\lim_{x\to 0}\frac{\sin x}{x} = 1$$
임을 이용하면 연속이다.
(나)
분자의 차수가 분모의 차수보다 크므로 원점으로의 극한값이 $0$이다. 따라서 연속이다.
(다)
$$\lim_{x\to 0}\frac{1}{x^2}e^{-\frac{1}{x^2}} = 0$$
임을 이용하면 연속이다.
이상에서 연속인 함수의 개수는 3이다.
2016 중앙대학교 편입수학 기출문제 25번 풀이
변수변환
$$\begin{cases}
x-2=u\\
y+1=\frac{v}{\sqrt{2}} \\
z+1=\frac{w}{\sqrt{3}}
\end{cases}$$
을 이용하면 주어진 문제는 제약조건
$$u+\frac{v}{\sqrt{2}} + \frac{w}{\sqrt{3}} = 11$$
에서 함수
$$u^2 + v^2 + w^2-9$$
의 최솟값을 구하는 문제가 된다.
이제
$$u^2 + v^2 + w^2-9 = k$$
라 하면
$$u^2 + v^2 + w^2 = (\sqrt{k+9})^2$$
와 같으므로, $k$가 최소가 되는 상황은 중심이 원점이고 반지름이 $\sqrt{k+9}$인 구가 평면
$$u+\frac{v}{\sqrt{2}} + \frac{w}{\sqrt{3}} = 11$$
에 접할 때이다.
따라서 원점에서 저 평면까지의 거리를 구해보면
$$d= \frac{11}{\sqrt{1+\frac{1}{2}+\frac{1}{3}}} = \sqrt{66}$$
에서
$$\sqrt{k+9}=\sqrt{66}$$
이므로 $k=57$이다.
2016 중앙대학교 편입수학 기출문제 26번 풀이
점 $(-1,2,1)$에서 두 곡면의 경도벡터를 구해보면 각각
$$v_1 = \begin{pmatrix}
-2 \\
-1 \\
2
\end{pmatrix}, v_2 = \begin{pmatrix}
-4 \\
2 \\
1
\end{pmatrix}$$
이므로, 이 둘을 외적하여 얻은 벡터를 구해보면
$$v = \begin{pmatrix}
5 \\
6 \\
8
\end{pmatrix}$$
이다.
따라서 구하는 접선은 벡터 $v$를 방향벡터로 하고 점 $(-1,2,1)$을 지나므로
선택지에서 찾아보면 정답은 4번이다.
2016 중앙대학교 편입수학 기출문제 27번 풀이
부분적분을 이용하면 주어진 적분은
$$\begin{align}
\text{(Integral)} &= f(x)f''(x)\bigg|_a^b - \frac{1}{2}\int_a^b f'(x)f''(x)dx \\
&= 3 - \frac{1}{2}(f'(x))^2 \bigg|_a^b \\
&= \frac{3}{2}
\end{align}$$
이다.
2016 중앙대학교 편입수학 기출문제 28번 풀이
$f(1)=3, f(2)=5, f(3)=7$이라는 조건을 잘 바라보면 곡선 $y=f(x)$가 세 점
$$(1, 3), (2, 5), (3, 7)$$
을 모두 지난다. 이때 이 세 점을 직선 $y=2x+1$도 전부 지나므로 인수정리를 이용하면
$$f(x)-(2x+1)=a(x-1)(x-2)(x-3)$$
을 만족시킨다.
이제 $f(0)=2$를 이용하면 $a=-\frac{1}{6}$이므로
$$f'''(1) = 6a = -1$$
이다.
2016 중앙대학교 편입수학 기출문제 29번 풀이
(가)
일차독립인 $n$개의 고유벡터를 가져도 되므로 거짓이다.
(나)
서로 다른 고유치에 대응하는 고유벡터는 일차독립이므로, 서로 다른 고유치에 대응하는 고유공간의 교집합은
영성분 뿐이다. 따라서 참이다.
(다)
각각의 고유치에 대해 대수적 중복도와 기하학적 중복도가 같다는 말이므로 참이다.
이상에서 옳은 것의 개수는 2이다.
2016 중앙대학교 편입수학 기출문제 30번 풀이
수렴반지름이 $1$임은 바로 알 수 있으므로 $x=1$에서의 수렴성만 확인하면
정답을 3, 4번 중 확정할 수 있고, $x=1$인 경우 주어진 급수는
$$\sum_{n=2}^{\infty} \frac{(-1)^n}{\ln n}$$
이고 이는 교대급수 판정법으로부터 수렴한다.
따라서 정답은 3번이다.
마치며
이상으로 2016 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설을 마치겠습니다.
오류, 오타 또는 궁금하신 점이 있으시면 댓글로 남겨주세요~
년도별 중앙대학교(수학과) 편입수학 정답 및 해설 (클릭시 이동)
2014년 및 그 이후의 시험지를 다룹니다.
별도로 기재되어 있지 않은 년도의 시험지의 경우 제 블로그의 '중앙대' 카테고리를 확인하세요.
- 2017 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설
- 2018 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설
- 2019 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설
- 2020 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설
- 2021 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설
- 2022 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설
- 2023 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설
- 2024 중앙대학교 편입수학 기출문제 정답 및 해설
'편입수학 기출문제 풀이 > 중앙대(공대 및 수학과)' 카테고리의 다른 글
| [편입] 2018 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설 (풀이) (1) | 2025.01.01 |
|---|---|
| [편입] 2017 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2025.01.01 |
| [편입] 2015 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설 (풀이) (1) | 2025.01.01 |
| [편입] 2014 중앙대학교(수학과) 편입수학 기출문제 정답 및 해설 (풀이) (0) | 2025.01.01 |
| [편입] 2024 중앙대학교 편입수학 기출문제 정답 및 해설 (풀이) (10) | 2024.04.01 |