[편입] 2024 세종대학교 편입수학 기출문제 정답 및 해설 (풀이)
안녕하세요 수학올인입니다.
이번 포스팅에선 2024년 세종대학교 편입수학 기출문제의 정답과 풀이를 다뤄보겠습니다.
풀이는 전부 제 풀이이며, 따라서 오타나 오류가 있을 수 있습니다.
원본 시험지는 제가 공유하지 않으며, 세종대학교 입학처에서 확인하실 수 있습니다.
(세종대학교 입학처 - 기출문제 - 편입학)
2024 세종대학교 편입수학 기출문제 빠른 정답
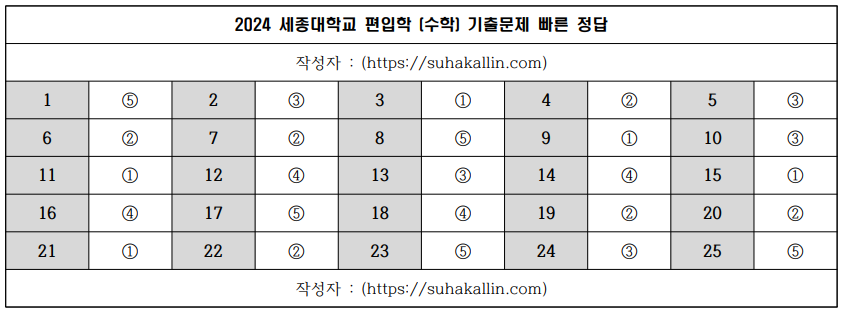
빠른 정답은 위 사진을 참고해 주시고, 아래는 문항별 풀이입니다.
2024 세종대학교 편입수학 기출문제 1번 풀이
직접 편미분해보면
$$f_x(x, y) = 2x\cosh(x^2 + y)$$
이므로, 구하는 값은 $e + \frac{1}{e}$이다.
2024 세종대학교 편입수학 기출문제 2번 풀이
$(x-1)^2 = X$로 치환하면 주어진 급수는
$$\sum_{n=1}^{\infty} \frac{X^n}{4^n}$$
와 같은데, 이 급수의 수렴반지름이 $4$이다.
즉,
$$(x-1)^2 < 4 \quad \Longrightarrow\quad |x-1|<2$$
이므로, 구하는 급수의 수렴반지름은 $2$이다.
2024 세종대학교 편입수학 기출문제 3번 풀이
$e^x$로 묶어낸 뒤 $e$의 정의를 이용하면 주어진 극한은
$$\begin{align}
\text{(Limit)} &= \lim_{x\to\infty} e(1+x^2 e^{-x})^{\frac{1}{x}} \\
&= \lim_{x\to\infty} e(1+x^2 e^{-x})^{\frac{1}{x^2 e^{-x}}\times \frac{x^2 e^{-x}}{x}} \\
&= e\times e^0 \\
&= e
\end{align}$$
이다.
2024 세종대학교 편입수학 기출문제 4번 풀이
[풀이 1]
$n$이 충분히 클 때 다음이 성립한다.
$$\sum_{k=1}^n k^p \approx \int_0^n x^p dx =\frac{n^{p+1}}{n+1}$$
이를 이용하면 주어진 극한은 근사적으로
$$\lim_{n\to\infty} \frac{1}{n^6}\times \frac{n^6}{6}$$
와 같으므로, 구하는 극한값은 $\frac{1}{6}$이다.
[풀이 2]
식을 적절히 변형한 뒤 급수를 정적분으로 고치면 주어진 극한은
$$\begin{align}
\text{(Limit)} &= \lim_{n\to\infty} \frac{n^6}{n^6 + n}\times \frac{1}{n}\sum_{k=1}^n \left(\frac{k^5 + k^4}{n^5}\right) \\
&= 1\times \left(\int_0^1 x^5 dx + 0\times \int_0^1 x^4 dx \right) \\
&= \int_0^1 x^5 dx \\
&= \frac{1}{6}
\end{align}$$
이다.
2024 세종대학교 편입수학 기출문제 5번 풀이
적분구간이 대칭적이므로 대칭성을 이용하자. 함수
$$\frac{1+2|x|}{1+|x|+x^2}$$
은 우함수이고 함수
$$\frac{\tan x}{1+|x|+x^2}$$
은 기함수이므로 주어진 적분은
$$\begin{align}
\text{(Integral)} &= \int_{-1}^1 \frac{1+2|x|}{1+|x|+x^2} dx \\
&= 2\int_0^1 \frac{1+2x}{1+x+x^2}dx \\
&= 2\ln(1+x+x^2)\bigg|_0^1 \\
&= 2\ln 3
\end{align}$$
이다.
2024 세종대학교 편입수학 기출문제 6번 풀이
$f(x)$의 분자 분모에 $e^x$를 곱하여 식을 정리하면
$$f(x) = \frac{e^x}{e^x + 1}$$
이다. 이제 방정식
$$f(x) = \frac{2}{3}$$
의 실근을 $a$라 하면
$$\frac{e^a}{e^a + 1}=\frac{2}{3}\quad\Longrightarrow\quad e^a = 2$$
가 성립한다.
이제 미분하면
$$f'(x) = \frac{e^x(e^x + 1) - e^{2x}}{(e^x + 1)^2}$$
에서 $x=a$를 대입하면 (즉, $e^a = 2$임을 이용하면)
$$f'(a) = \frac{6-4}{9} = \frac{2}{9}$$
이다.
2024 세종대학교 편입수학 기출문제 7번 풀이
가장 먼저
$$\sin^{-1}\left(\frac{\sqrt{3}}{2}\right) = \frac{\pi}{3}$$
임은 바로 알 수 있다.
다음으로 $\frac{5}{9}\pi > \frac{\pi}{2}$이므로
$$\begin{align}
\tan^{-1}\tan\left(\frac{5}{9}{\pi}\right) &= \tan^{-1}\tan\left(\frac{5}{9}{\pi} - \pi\right) \\
&= \tan^{-1}\tan\left(-\frac{4}{9}{\pi}\right) \\
&= -\frac{4}{9}\pi
\end{align}$$
이다. 따라서 구하는 값은 $-\frac{\pi}{9}$이다.
2024 세종대학교 편입수학 기출문제 8번 풀이
5번의 경우 $n$이 충분히 크다면 항상
$$(\ln n)^3 < \sqrt{n}$$
이도록 할 수 있으므로 어떤 자연수 $N$에 대하여
$$\sum_{n=N}^{\infty} \frac{1}{\sqrt{n}(\ln n)^3} > \sum_{n=N}^{\infty} \frac{1}{n}$$
이도록 할 수 있다. 따라서 비교판정법으로부터 5번의 급수는 발산한다.
2024 세종대학교 편입수학 기출문제 9번 풀이
ㄱ. $p$판정법으로부터 수렴한다.
ㄴ. $x=1$근방에서 $\ln x \approx x-1$이므로 주어진 적분은
$$\int_1^e \frac{1}{x-1}dx $$
와 수렴 발산 여부가 같은데 이 적분이 발산함은 쉽게 알 수 있다.
ㄷ. $p$판정법으로부터 발산한다.
이상에서 수렴하는 특이적분은 ㄱ뿐이다.
2024 세종대학교 편입수학 기출문제 10번 풀이
행렬 $A$의 고유치를 구해보면
$$\lambda = -2, -1, 1$$
이므로
$$f(n) = \text{tr}(A^n) = (-2)^n + (-1)^n + 1$$
이다. 이제 부등식 $f(n+1) - f(n) > 2024$를 다시 써보면
$$\begin{align}
f(n+1) - f(n) &= (-2)\times (-2)^n - (-1)^n - (-2)^n - (-1)^n \\
&= (-3)\times(-2)^n - 2\times(-1)^n \\
&\geq 2024
\end{align}$$
이다.
이때 만약 $n$이 짝수라면 $(-2)^n$이 양수가 되어 전체 식은 음수가 된다.
따라서 $n$은 홀수이고, 대충 어느정도의 $n$을 잡아야 하는지 확인해보기 위해 $\frac{2024}{3}$을 계산해보면
$$\frac{2024}{3} \approx 674.\cdots$$
이고 $2^9 = 512 < 674$이므로 구하는 최소의 자연수 $n$은 11이다.
2024 세종대학교 편입수학 기출문제 11번 풀이
$e$의 정의를 이용하여 풀이할 것인데, 지수가 $n$이므로 괄호 안의 식은
$\frac{1}{n}$와 같은 속도인 식만 의미가 있다.
즉, 괄호 내부의 $\frac{x^3}{n\sqrt{n}}$은 무시하고 풀어도 된다.
따라서 주어진 극한은
$$\begin{align}
\text{(Limit)} &= \lim_{n\to\infty}\left(1 - \frac{x^2}{2n}\right)^{-\frac{x^2}{2n}\times n} \\
&= e^{-\frac{x^2}{2}}
\end{align}$$
이고 이 식이 곧 $f(x)$이다. 따라서 미분해보면
$$f'(x) = -xe^{-\frac{x^2}{2}}$$
이므로 구하는 값은 $-\frac{2}{e^2}$이다.
2024 세종대학교 편입수학 기출문제 12번 풀이
[풀이 1]
주어진 식을 변형하여 완전제곱식들의 합으로 써보면
$$\begin{align}
f(x, y) &= -\left(\sqrt{3}y - \frac{2}{\sqrt{3}}x\right)^2 - \frac{2}{3}x^2 + 4x + 1 \\
&= -\left(\sqrt{3}y - \frac{2}{\sqrt{3}}x\right)^2 - \frac{2}{3}(x-3)^2 + 7
\end{align}$$
이라 쓸 수 있다.
이때 주어진 식은 항상 $7$이하의 값을 가지고, $x, y$의 값을 조절하여 $7$이 되게 할 수 있으므로
맞는 선지는 '극댓값은 7이다' 이다.
[풀이 2]
일반적인 극값을 찾는 방법대로 편미분하여 계산한다.
(생략)
2024 세종대학교 편입수학 기출문제 13번 풀이
삼배각 공식과 테일러전개를 이용하면
$$\begin{align}
\sin^3 x &= \frac{1}{4}(3\sin x-\sin 3x) \\
&= \cdots + \frac{1}{4}\left(-\frac{3}{7!} + \frac{3^7}{7!}\right)x^7 + \cdots
\end{align}$$
이므로, 구하는 값은 $x^7$의 계수에 $7!$을 곱한 $546$이다.
2024 세종대학교 편입수학 기출문제 14번 풀이
주어진 점에서의 경도벡터를 구하기 위해 편도함수를 각각 구해보면
$$\begin{align}
& f_x = 4x + 2y - 2z \\
& f_y = 4y + 2x + 2z \\
& f_z = 6z + 2y - 2x
\end{align}$$
이므로, 주어진 점에서 함수 $f$의 경도벡터는
$$\nabla f =(8,4,-6)$$
이다.
이제 선지의 벡터와 경도벡터를 내적하여 음수가 되는 벡터의 개수를 찾자.
(구체적 크기가 아닌 부호 여부만 조사하면 되므로 $v_i$들의 크기를
$1$로 만들지 않아도 된다.)
보기의 벡터들과 전부 내적해보면 1, 2, 3, 4번 순서대로 내적의 결과가
음수, 음수, 음수, 양수이므로, 감소하는 방향이 되는 벡터의 수는 3이다.
2024 세종대학교 편입수학 기출문제 15번 풀이
주어진 행렬이 $n\times n$행렬이라고 가정하자.
첫 번째 등식으로부터
$$2^{n+4}\det A = 2^{2n}\det A$$
가 성립하고, 이는 곧 $n=4$임을 의미한다.
다음으로 두 번째 등식으로부터
$$4\det A = (\det A)^3$$
에서 $(\det A)^2 = 4$가 성립한다.
따라서 행렬식의 성질을 이용하면 구하는 값은
$$\det (A^{-2}) = \frac{1}{(\det A)^2} = \frac{1}{4}$$
이다.
2024 세종대학교 편입수학 기출문제 16번 풀이
구면좌표계를 이용하면 주어진 삼중적분은
$$\begin{align}
\text{(Integral)} &= \int_0^{2\pi} \int_0^{\frac{\pi}{2}} \int_1^2 \rho^3 \sin\phi\cos\phi d\rho d\phi d\theta\\
&= 2\pi \times \frac{1}{2}\times \frac{15}{4} \\
&= \frac{15}{4}\pi
\end{align}$$
이다.
2024 세종대학교 편입수학 기출문제 17번 풀이
$\frac{1}{x} = t$로 치환하면 주어진 적분은
$$\begin{align}
\text{(Integral)} &= \int_{\frac{1}{2}}^2 \frac{1-2t}{t^2 + 1}dt \\
&= \tan^{-1} 2 - \tan^{-1}\left(\frac{1}{2}\right) - \ln 4
\end{align}$$
이다. 그런데 일치하는 선지가 존재하지 않는다.
이제 $\tan a = 2, \tan b = \frac{1}{2}$라 하면 덧셈정리로부터
$$\begin{align}
\tan(a-b) &= \frac{\tan a - \tan b}{1+\tan a\tan b} \\
&= \frac{3}{4}
\end{align}$$
에서 양변에 $\tan^{-1}$을 씌우면
$$a-b = \tan^{-1}2 - \tan^{-1}\left(\frac{1}{2}\right) = \tan^{-1}\left(\frac{3}{4}\right)$$
이다. 따라서 정답은 5번이다.
2024 세종대학교 편입수학 기출문제 18번 풀이
주어진 구면의 단위법선벡터가 $n=(x,y,z)$임을 이용하자. 벡터장
$$F(x,y,z)=(x,y,z^2)$$
에 대하여 $F\circ n =x^2 + y^2 + z^3$이므로, 주어진 스칼라장에 대한 면적분은
벡터장 $F$에 대한 면적분으로 바꿀 수 있다.
이제 주어진 구면 $S$의 내부를 $E$라 하고 발산정리를 이용하면 주어진 면적분은
$$\begin{align}
\text{(Integral)} &= \iiint_E (2+2z)dV \\
&= \iiint_E 2 dV \\
&= \frac{8}{3}\pi
\end{align}$$
이다.
2024 세종대학교 편입수학 기출문제 19번 풀이
문제를 읽어보면 $\text{curl}F$를 면적분하므로 선적분 문제와 같다.
또, 주어진 곡면의 경계곡선은
1. 점 $(1,0,0)$에서 출발하여 $xy$평면 위의 원 $x^2 + y^2 = 1$을 따라 점 $(-1,0,0)$까지 이동
2. 점 $(-1,0,0)$에서 출발하여 $xz$평면 위의 원 $x^2 + 4z^2 = 1$을 따라 점 $(1,0,0)$까지 이동
로 바꿀 수 있으며 각각의 경로를 $C_1, C_2$라 하자.
두 경로를 각각 매개화하면
$$\begin{align}
r_1(t) &= (\cos t, \sin t, 0)\quad (t : 0\to \pi) \\
r_2(t) &= \left(\cos t, 0, \frac{\sin t}{2}\right) \quad (t : \pi\to 0)
\end{align}$$
이므로 두 경로에 대한 선적분값을 각각 구해보면
$$\begin{align}
\int_{C_1} F dr &= \int_0^{\pi}(\sin^3 t, ? ?)\circ (-\sin t, ?, ?)dt \\
&= \int_0^{\pi} -\sin^4 t dt \\
&= -\frac{3}{8}\pi
\end{align}$$
이고
$$\begin{align}
\int_{C_2} F dr &= \int_{\pi}^0 (?, ?, \cos^2 t)\circ \left(?, ?, \frac{\cos t}{2}\right)dt \\
&= \int_{\pi}^{0} \frac{\cos^3 t}{2}dt \\
&= 0
\end{align}$$
이다. (?로 표기된 항은 소거되는 항이므로 굳이 작성하지 않은 것이다)
따라서 구하는 값은 위의 두 선적분의 합인 $-\frac{3}{8}\pi$이다.
2024 세종대학교 편입수학 기출문제 20번 풀이
가장 먼저
$$(x^2 + y^2)^{\frac{3}{2}}=2xy \geq 0$$
임을 알 수 있다. 따라서 $xy \geq 0$이어야 하고 이는 곧
$$x\geq 0, y\geq 0$$
이거나
$$ x\leq 0, y\leq 0$$
이어야 함을 알 수 있다. 따라서 주어진 곡선은 제 1, 3사분면에 그려진다.
이제 극좌표를 이용하여 주어진 곡선을 다시 표현해보면
$$r=\sin2\theta$$
이므로 주어진 곡선은 4엽 장미곡선 중 잎사귀가 둘만 남아있는 곡선이다.
(4개의 잎사귀 중 제 1, 3사분면의 잎사귀만 남은 형태)
따라서 주어진 곡선으로 둘러싸인 넓이는 4엽 장미곡선 내부넓이의 절반일 것이므로
구하는 넓이 $S$는
$$S = \frac{1}{2}\times \frac{\pi}{2} = \frac{\pi}{4}$$
이다.
2024 세종대학교 편입수학 기출문제 21번 풀이
발산정리를 이용하면 주어진 면적분은
$$\begin{align}
\text{(Integral)} &= \iiint_E 21 dV \\
&= 21\int_{-1}^1 \int_{x^2}^{1} \int_{y^2}^{1} 1 dzdydx \\
&= 21\int_{-1}^1 \int_{x^2}^{1} (1-y^2)dydx \\
&= 21\int_{-1}^1 \left( 1-x^2 - \frac{1-x^6}{3}\right)dx \\
&= 42\int_0^1 \left( 1-x^2 - \frac{1-x^6}{3}\right)dx \\
&= 16
\end{align}$$
이다.
2024 세종대학교 편입수학 기출문제 22번 풀이
실수 $t$에 대하여 구하는 사면체의 부피를 $f(t)$라 하면
$$\begin{align}
f(t) &= \frac{1}{6}\left|\det \begin{pmatrix}
2 & \sec t & -1 \\
\sec t & -1 & -2 \\
2 & \sec t & 0
\end{pmatrix}\right| \\
&= \frac{\sec^2 t + 2}{6} \\
&\geq \frac{1+2}{6} \\
&= \frac{1}{2}
\end{align}$$
이므로 구하는 부피의 최솟값은 $\frac{1}{2}$이다.
2024 세종대학교 편입수학 기출문제 23번 풀이
[풀이 1]
기하적 관찰을 통해 풀이를 단순화 할 수 있다.
먼저 주어진 목표를 다시 쓰면
$$|\mathrm{OP}|\cos\theta$$
의 최소를 구하는 것과 같다. (단, $\theta$는 $\mathrm{OP}, \mathrm{OQ}$의 사잇각)
이때 $|\mathrm{OP}|$는 크기가 고정되어 있으므로 주어진 문제는 $\cos\theta$를 최소화하는 문제가 된다.
이제 다음과 같은 그림을 생각해보면, 둘의 사잇각 $\theta$는 $\mathrm{OQ}$가 주어진 포물면에 접하는 형태일 때
최대가 됨을 알 수 있다. (빨간색 직선)
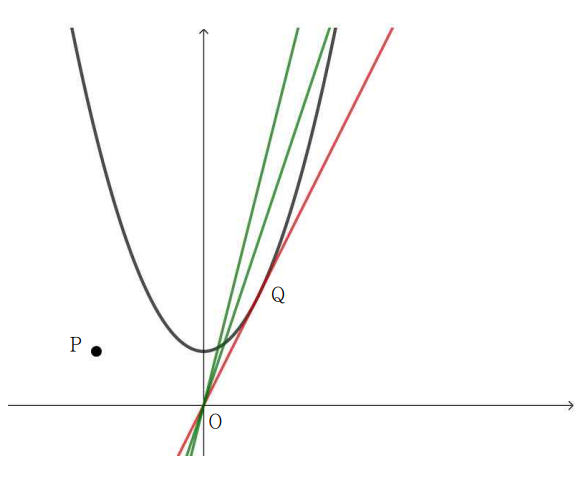
따라서 벡터 $\mathrm{OQ}$와 점 $\mathrm{Q}$에서의 경도벡터가 수직, 즉 내적이 0이므로
$$(x,y,z)\circ\left(\frac{x}{2}, y, -1\right) = \frac{x^2}{2} + y^2 - z = 0$$
임을 얻는다. 즉, 점 $\mathrm{Q}(x,y,z)$는 두 개의 관계식
$$z=\frac{x^2}{4} + \frac{y^2}{2} + 1,\quad \frac{x^2}{2} + y^2 - z = 0$$
을 전부 만족시켜야 하고, 둘을 합치면
$$\frac{x^2}{4} + \frac{y^2}{2} = 1$$
을 얻는다.
그런데 위의 제약조건을 만족시키는 점 $(x,y,z)$의 좌표는 매개변수 $t$를 통해
$$(x,y,z)=(2\cos t,\sqrt{2}\sin t, 2)$$
로 매개화 시킬 수 있다. ($z$좌표가 $2$인 것은 위에서 구한 두 번째 관계식에 대입하면 얻어진다.)
따라서
$$\begin{align}
\cos\theta &= \frac{\mathrm{OP}\circ \mathrm{OQ}}{|\mathrm{OP}|\times| \mathrm{OQ}|} \\
&= \frac{4\cos t + 2}{\sqrt{5}\times \sqrt{4\cos^2 t + 2\sin^2 t + 4}} \\
&= \frac{4\cos t + 2}{\sqrt{5}\times \sqrt{2\cos^2 t + 6}}
\end{align}$$
인데 함수
$$\frac{4x+2}{\sqrt{5}\times \sqrt{2x^2 + 6}}$$
은 $-1\leq x\leq 1$에서 증가하므로 $x$가 작을수록 함숫값도 작아진다.
이 말은 곧, 위의 식은 $\cos t = -1$일 때, 즉 $t=\pi$일 때 최솟값 $-\frac{1}{\sqrt{10}}$을 갖는다.
한편 $|\mathrm{OP}|=\sqrt{5}$로 고정되어 있으므로, 우리가 구하는 최소는
$$\sqrt{5}\times \left(-\frac{1}{\sqrt{10}}\right) = -\frac{1}{\sqrt{2}}$$
이다.
[풀이 2]
식을 이용해서 풀자.
구하는 목표를 전부 $x, y, z$에 대해 정리하면 우리의 목표는 제약조건
$$z=\frac{x^2}{4} + \frac{y^2}{2} + 1$$
하에서 함수
$$f(x,y,z) = \frac{2x+z}{\sqrt{x^2 + y^2 + z^2}}$$
의 최소를 구하는 문제가 되며 라그랑주 승수법을 이용해 문제를 해결할 수 있다.
(계산 생략)
2024 세종대학교 편입수학 기출문제 24번 풀이
좌변을 이차형식으로 나타냈을 때의 대칭행렬 $A$를 구해보면
$$A = \begin{pmatrix}
2 & \sqrt{2} \\
\sqrt{2} & 3
\end{pmatrix}$$
인데, 이 행렬의 고유치를 구해보면
$$\lambda = 1, 4$$
임을 알 수 있다. 따라서 곡선 $2x^2 + 2\sqrt{2}xy + 3y^2 = 36$은 주축정리로부터
$$x^2 + 4y^2 =36$$
이라는 타원을 회전시켜 얻은 곡선임을 알 수 있다.
이때 회전은 타원의 장축, 단축의 길이를 변화시키지 않으므로 아래 그림과 같은 상황에서
타원 내부에 포함되는 원의 반지름이 최대가 됨을 알 수 있다.
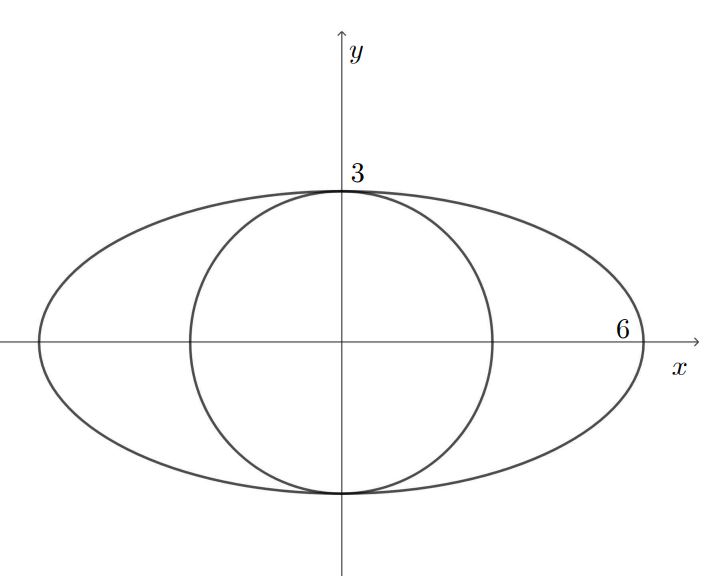
따라서 구하는 반지름의 최댓값은 $3$이다.
2024 세종대학교 편입수학 기출문제 25번 풀이
두 번째 식에서 첫 번째 식을 빼면
$$12y+24z = 55$$
임을 얻는다. 또, 첫 번째 식을 정리하면
$$x^2 = 14 - (2y^2 + 3z^2)$$
임을 얻는다. 이제 코시 슈바르츠 부등식을 이용하면
$$(2y^2 + 3z^2)\left(\left(\frac{12}{\sqrt{2}}\right)^2 + \left(\frac{24}{\sqrt{3}}\right)^2\right)\geq (12y+24z)^2$$
가 성립하는데, 이 식을 정리하면
$$2y^2 + 3z^2 \geq \frac{275}{24}$$
이다. 한편 위에서 얻은 식을 이용하면
$$\begin{align}
x^2 &= 14 - (2y^2 + 3z^2) \\
&\leq 14 - \frac{275}{24} \\
&= \frac{61}{24}
\end{align}$$
가 구하는 최댓값이 된다.
마치며
이상으로 2024 세종대학교 편입수학 기출문제 정답 및 해설을 마치겠습니다.
오류, 오타 또는 궁금하신 점이 있으시면 댓글로 남겨주세요~
년도별 세종대학교 편입수학 정답 및 해설
(클릭시 이동)
- 2017 세종대학교 편입수학 정답 및 해설
- 2018 세종대학교 편입수학 정답 및 해설
- 2019 세종대학교 편입수학 정답 및 해설
- 2020 세종대학교 편입수학 정답 및 해설
- 2021 세종대학교 편입수학 정답 및 해설 (오전)
- 2021 세종대학교 편입수학 정답 및 해설 (오후)
- 2022 세종대학교 편입수학 정답 및 해설
- 2023 세종대학교 편입수학 정답 및 해설
- 2024 세종대학교 편입수학 정답 및 해설 (현재)
'편입수학 기출문제 풀이 > 세종대' 카테고리의 다른 글
| [편입] 2025 세종대학교 편입수학 기출문제 정답 및 해설 (풀이) (1) | 2025.04.08 |
|---|---|
| [편입] 2023 세종대학교 편입수학 기출문제 정답 및 해설 (풀이) (21) | 2023.11.12 |
| [편입] 2022 세종대학교 편입수학 기출문제 정답 및 해설 (풀이) (2) | 2023.11.11 |
| [편입] 2021 세종대학교(오후) 편입수학 기출문제 정답 및 해설 (풀이) (1) | 2023.11.03 |
| [편입] 2021 세종대학교(오전) 편입수학 기출문제 정답 및 해설 (풀이) (2) | 2023.11.02 |